
Question and Answers Forum
AllQuestion and Answers: Page 557









Pg 552 Pg 553 Pg 554 Pg 555 Pg 556 Pg 557 Pg 558 Pg 559 Pg 560 Pg 561
|
Question and Answers Forum |
AllQuestion and Answers: Page 557 |

|

|

|
| if x;y;z≥0 then: 2 Σ_(cyc) x^2 (x^2 + y^2 ) ≥ Σ_(cyc) x(x^3 + z^3 ) + xyz(x+y+z) |
| Solve for real numbers: x^(32) + x^(16) + y^2 = 2 (√2) x^(12) y |

|

|

|
| 82,1336,18670,240004,2933338,34666672,400000006,? is there a valid pattern for these numbers? |
| soit:F={(x,y,z)∈R^3 /x−y−2z} et G=Vect(0,1,1) determiner l′intersection de F et G |
| Given x,y∈R^+ and ((x/5)+(y/3))((5/x)+(3/y))=139. If maximum and minimum of ((x+y)/( (√(xy)) )) is M and n respectively, then what the value of 3M−4n. |

|
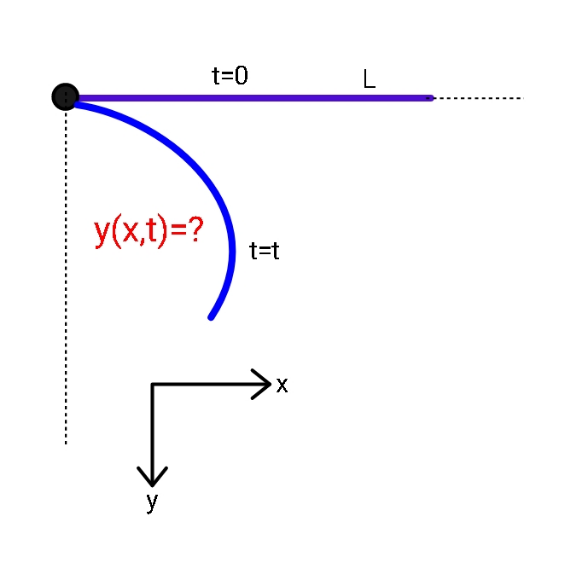
| EI(∂^4 y/∂x^4 )+ρS(∂^2 y/∂t^2 )=0 (1) y(x,0)=U_0 (x) (∂y/∂t)(x,0)=V_0 (x) ; EI(∂^2 y/∂x^2 )(0,t)=EI(∂^2 y/∂x^2 )(L,t)=0 |
| Prove that: (((x-1)^2 )/x) + ((x+1)/( (√(x^2 +1)))) ≥ (√2) ; ∀x>0 |
| Prove that: (((x-1)^2 )/x) + ((x+1)/( (√(x^2 +1)))) ≥ 2 ; ∀x>0 |
| Prove that 5 divide n(4n^2 + 1)(6n^2 + 1) for any natural number n |
| Solve for complex numbers: x^4 + (1 + i)x^3 + 2ix^2 + (i - 1)x - 1 = 0 |
| ∫(1/(1+ln x))dx=? |

|
| source: myself x^5 +3cx^2 −x−5c=0 |
| ∫((5x^3 −3x^2 +7x−3)/((x^2 +1)^2 ))dx Solve by first finding the partial fraction |

|

|
| (1) lim_(x→0) (((e^x −1)sin x+tan^3 x)/(arctan x ln (1+4x)+4arcsin^4 x)) (2) lim_(x→0) ((1−cos x+ln (1+tan^2 2x)+2arcsin^3 x)/(1−cos 4x+sin^2 x)) |
| lim_(x→∞) (sin (√(x+1))−sin (√(x ))) =? |
| lim_(n→∞) Σ_(k=1) ^n (1/n).e^((2k+1)/k) =? |
Pg 552 Pg 553 Pg 554 Pg 555 Pg 556 Pg 557 Pg 558 Pg 559 Pg 560 Pg 561 |