
Question and Answers Forum
AllQuestion and Answers: Page 570
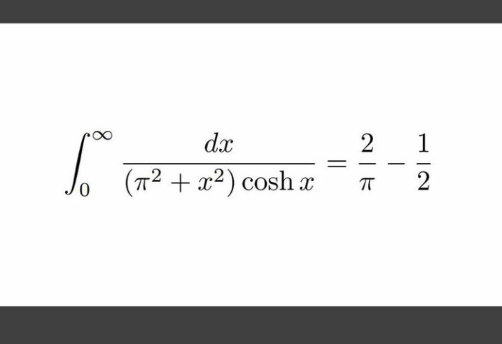
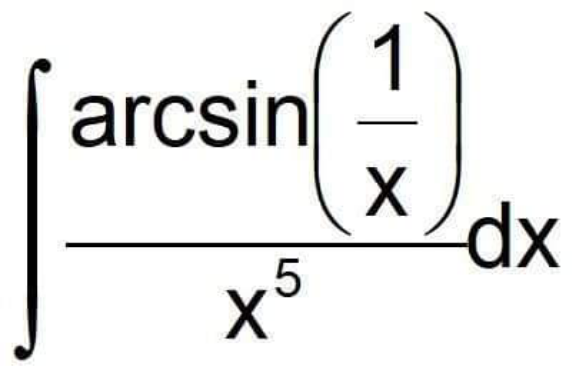
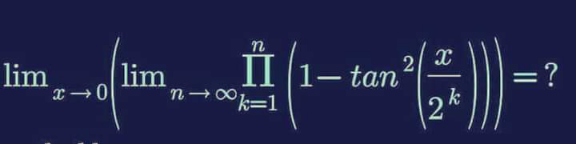
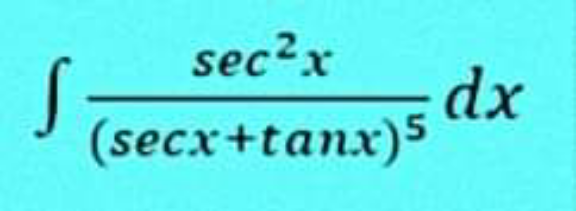







Pg 565 Pg 566 Pg 567 Pg 568 Pg 569 Pg 570 Pg 571 Pg 572 Pg 573 Pg 574
|
Question and Answers Forum |
AllQuestion and Answers: Page 570 |
| find the value of x and y, x:3:5=8:y:9 |
| find the value of x and y , x:3:5=2:y:10 |
| Ω_1 = 1 - (π/2) +Σ_(n=2) ^∞ (- (1/𝛑))^n ∙ (1/(n+1)) Ω_2 = 1 - (π/2) + Σ_(n=2) ^∞ (- (1/e))^n ∙ (1/(n+1)) A) Ω_1 < Ω_2 B) Ω_1 = Ω_2 C) Ω_1 > Ω_2 |
| (dy/dx)−(x/y)+x^3 cos y = 0 |
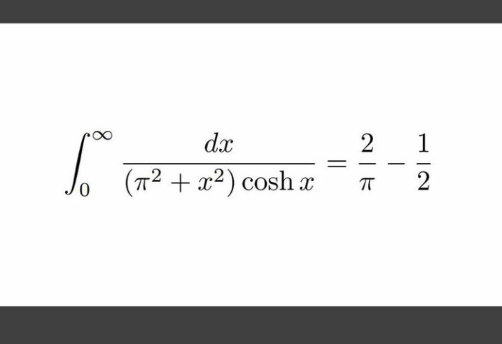
|
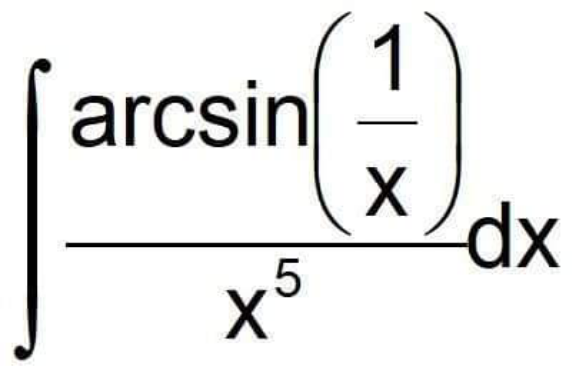
|
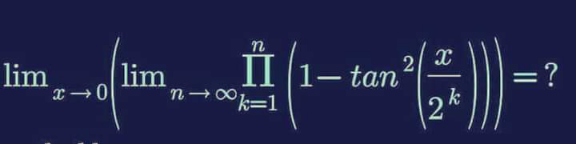
|
| tan 2x tan 3x tan 5x =1 |
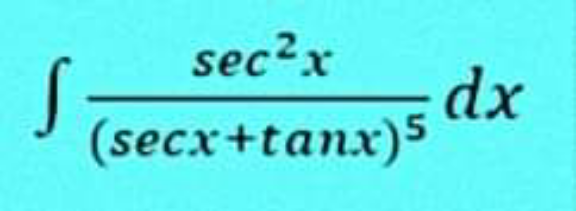
|

|
| φ := ∫_0 ^( 1) (( ln (1−x^( 2) ))/(1+ x^( 2) )) dx = proof : φ = ∫_0 ^( 1) (( ln(1−x ))/(1+x^( 2) ))dx + (π/8)ln(2) .... I= ∫_0 ^( 1) ((ln ( 1−x ))/(1+x^( 2) ))dx =^(x=tan(t)) ∫_0 ^( (π/4)) ln( cos(t)−sin(t))dt−∫_0 ^( (π/4)) ln(cos(t))dt = ∫_0 ^( (π/4)) ln((√2) )dt +∫_0 ^( (π/4)) ln(sin((π/4) −t))dt−(G/2) +(π/4)ln(2) =((3π)/8) ln(2)−(G/2) −(G/2) −(π/4) ln(2)=(π/8)ln(2)−G φ = (π/4)ln(2) − G ■ m.n |
| ∫_0 ^∞ ((x)^(1/n) /(x^3 +x^2 +x+1))dx=? |
| (dy/dx) = ((y^3 −xy^2 −x^2 y−5x^3 )/(xy^2 −x^2 y−2x^3 )) |
| 𝛀 =∫_( 0) ^( 1) ∫_( 0) ^( 1) ((log(1 - x) log(1 - y))/(1 - xy)) dxdy = ? |
| 𝛀 =Σ_(n=0) ^∞ Σ_(k=0) ^n (1/𝛑^n ) ∙ ((π/e))^k = ? |

|
| ∫_0 ^1 ((ln(e+(1/(1−t))))/( (√t)))dt=? |

|

|

|
| If x − z = tan^(− 1) (yz) and z = z(x, y), find ((δz)/(δx)) , ((δz)/(δy)) |
| ∫ (dx/((x^2 −x+1)((√(x^2 +x+1))))) |

|
| Solve in R x^2 + 4x = (√(40x^2 + 32x - 16)) |
| Find: 𝛀 =∫ ((x^7 - x^5 + x^3 - x)/(1 + x^(10) )) dx ; x∈R |

|
Pg 565 Pg 566 Pg 567 Pg 568 Pg 569 Pg 570 Pg 571 Pg 572 Pg 573 Pg 574 |