
Question and Answers Forum
AllQuestion and Answers: Page 572
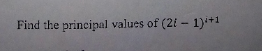




Pg 567 Pg 568 Pg 569 Pg 570 Pg 571 Pg 572 Pg 573 Pg 574 Pg 575 Pg 576
|
Question and Answers Forum |
AllQuestion and Answers: Page 572 |
| Ω=∫_0 ^( ∞) log(sinh(x)).log(tanh(x))dx=((7ζ(3))/8) +(π^( 2) /8)ln^ (2) |
| Show that tan^(− 1) ((1/3)) + sin^(− 1) ((1/3)) = (π/4) |
| Find the nth root of 1. Find these values when n = 6. |
| Prof that: Σ_(n=1) ^(10) n.n!=11!−1 |
| prove that: ∫_0 ^( 1) ∫_0 ^( 1) (((√x) +(√y))/((1−xy)((xy))^(1/4) )) dxdy=4 (4 −π) |
|
| Find this excercise about limits trigonometri 1). lim_(θ→0) ((2cos θ−2)/(3θ)) 2). lim_(x→0) ((1−cos x)/x^(2/3) ) 3). lim_(t→0) ((4t^2 +3t sin t)/t^2 ) 4). lim_(x→0) ((x^2 +1)/(x+cos x)) 5). lim_(x→0) ((sin^2 ((x/2)))/(sin x)) |
| Σ_(n=1) ^∞ (n ln(((2n+1)/(2n−1))) −1)=? |
| f is a function that assigns to each natural number multiplication of its digits for exampl : f( 200)=0 f ( 128 )=1×2×8 =16 find the value of : f (100) + f(101 )+ f (102 )+...f(999)=? |
| How many of the number formed by using all the digits 1,2,3,4,5,6 only once divisible by 25. |
| Use algebraic simplifications to help find the limits, if they exist. 1). lim_(x→2) ((x^2 −4)/(x−2)) 2). lim_(x→1) ((x^2 −x)/(2x^2 +5x−7)) 3). lim_(x→1) ((3x^2 −13x−10)/(2x^2 −7x−15)) 4). lim_(x→1) ((3x^2 −13x−10)/(2x^2 −7x−15)) 5). lim_(x→2) ((x^3 −8)/(x^2 −4)) |
| Given a rational function f(x) = ((ax^2 +bx+c)/(x+q)) has minimum point at (−2,9) and maximum point at (2,1) . Find value of a, b, c, and q . |
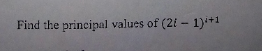
|

|
| Verify the identity in Excercise below 1). cos θsec θ=1 2). (1+cos β)(1−cos β)=sin^2 β 3). cos^2 x(sec^2 x−1)=sin^2 x 4). ((sin t)/(cosec t))+((cos t)/(sec t))=1 5). ((cosec^2 θ)/(1+tan^2 θ)) = cot^2 θ |
| Given that f○g = (x^2 /(2x^2 − x + 4)) and g(x) = (x/(x − 2)), find f(x) ? |

|
| proof that Σ_(n=1) ^(10) n×n! = 11!−1 |
| find the value of 2×1!+4×2!+6×3!+...+200×100! |
| { ((m^2 =n+2)),((n^2 =m+2)) :} ⇒m≠n 4mn−m^3 −n^3 =? |
| a,b,c,d,e (kids) are in ascending order of heights. If they are to stand in a circle in a way so that the sum of ∣difference in heights of adjacent pairs∣ is a minimum, find this minimum. |

|
| if x;y>0 then prove that: ((x^2 (1+xy)^2 +x^2 y^4 (1+x)^2 +(1+y)^2 )/(1 + xy + x^2 y + xy^2 )) ≥ 3xy |

|

|
| ∫_0 ^( 1) ln((sin(x)+cos(x))^2 +1) dx |
Pg 567 Pg 568 Pg 569 Pg 570 Pg 571 Pg 572 Pg 573 Pg 574 Pg 575 Pg 576 |