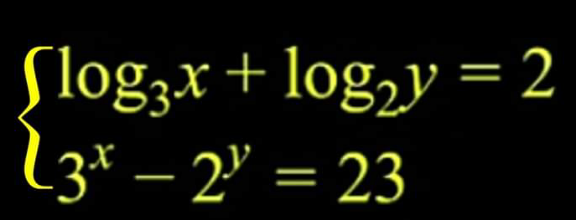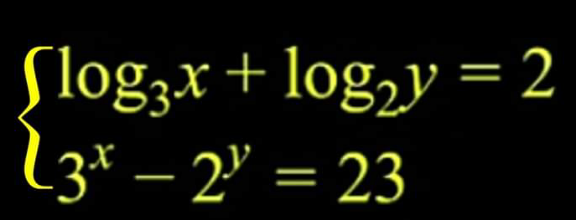Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 573

Question Number 155757 Answers: 0 Comments: 3

2x^2 (dy/dx) − 2x^2 = (x−1) y^2 ; y(1) = 2 □ M

$2 x^{2} \frac{d y}{d x} - 2 x^{2} = (x - 1) y^{2}; y (1) = 2$ $◻ M$

Question Number 155745 Answers: 2 Comments: 0

Σ_(k=1) ^n ((k/((4k^2 −1)(2k+3))))=?

$\underset{k = 1}{\sum^{n}} (\frac{k}{({4 k}^{2} - 1) (2 k + 3)}) = ?$

Question Number 155736 Answers: 0 Comments: 0

Question Number 155735 Answers: 1 Comments: 0

Question Number 155729 Answers: 1 Comments: 0

A={(a,b)∈IR^2 / a^2 +b^2 ≤1} prove that A can′t be written as the cartesian product of two parts of IR.

$A = {(a, b) \in {IR}^{2} / a^{2} + b^{2} ⩽ 1}$ $prove that A {can}^{'} t be written as the cartesian$ $product of two parts of IR .$

Question Number 155724 Answers: 1 Comments: 0

Find: (1/(sin^2 6^° )) + (1/(sin^2 42°)) + (1/(sin^2 66°)) + (1/(sin^2 78°)) = ?

$Find :$ $\frac{1}{\sin^{2} 6^{°}} + \frac{1}{\sin^{2} 42 °} + \frac{1}{\sin^{2} 66 °} + \frac{1}{\sin^{2} 78 °} = ?$

Question Number 155720 Answers: 3 Comments: 1

Question Number 155776 Answers: 0 Comments: 0

if x∈(0;(π/2)) then prove that: ((2 + (1+cotx)(tan^3 x+cot^3 x))/((1+tanx)(1+cotx))) ≥ (3/2)

$if x \in (0; \frac{π}{2}) then prove that :$ $\frac{2 + (1 + \cot x) (\tan^{3} x + \cot^{3} x)}{(1 + \tan x) (1 + \cot x)} ⩾ \frac{3}{2}$

Question Number 155710 Answers: 3 Comments: 1

lim_(x−oo) (1/(n(√n))) Σ_(k=1) ^n E((√(k)))

$li \underset{x - o o}{m} \frac{1}{n \sqrt{n}} \underset{k = 1}{\sum^{n}} E (\sqrt{k)}$

Question Number 155701 Answers: 0 Comments: 3

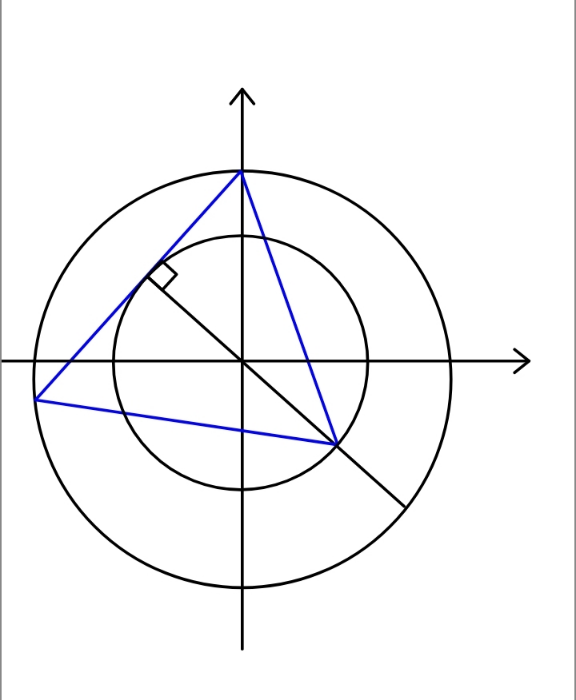
Question Number 155692 Answers: 1 Comments: 5

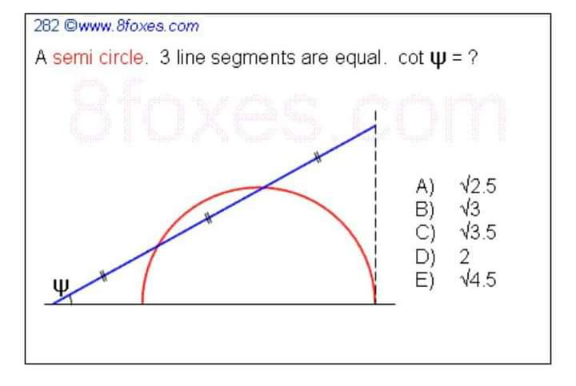
Question Number 155686 Answers: 2 Comments: 0

∫_0 ^(π/2) (dx/(1+tan x)) =?

$\int_{0}^{π / 2} \frac{d x}{1 + \tan x} = ?$

Question Number 155677 Answers: 1 Comments: 1

Question Number 155674 Answers: 0 Comments: 0

monster integral ∫_0 ^( (π/4)) ln^2 (sin(2x)+ cos(3x)) dx

$\underset{―}{monster integral}$ $\int_{0}^{\frac{π}{4}} \ln^{2} (\sin (2 x) + \cos (3 x)) d x$

Question Number 155673 Answers: 0 Comments: 0

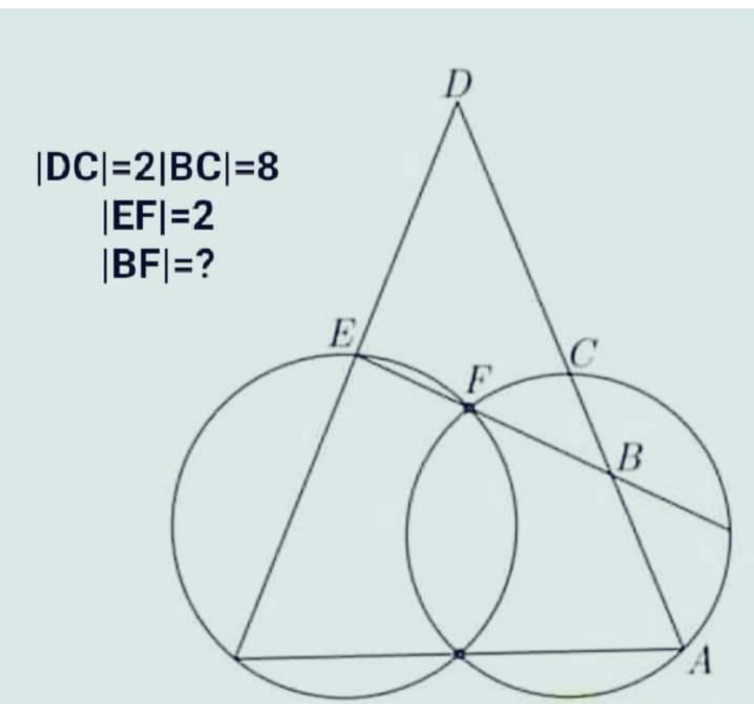
Question Number 155667 Answers: 0 Comments: 2

Question Number 155657 Answers: 2 Comments: 1

Question Number 155653 Answers: 0 Comments: 0

if a;b;c≥0 and a+b+c=1 prove that 18 Σ ab + 45 Σ a^2 b ≤ 11

$if a; b; c ⩾ 0 and a + b + c = 1 prove that$ $18 Σ ab + 45 Σ a^{2} b ⩽ 11$

Question Number 155650 Answers: 2 Comments: 0

Solve for real numbers: (√((x-a)/(x-b))) + (a/x) = (√((x-b)/(x-a))) + (b/x) a;b∈R and a≠b

$Solve for real numbers :$ $\sqrt{\frac{x - a}{x - b}} + \frac{a}{x} = \sqrt{\frac{x - b}{x - a}} + \frac{b}{x}$ $a; b \in R and a \neq b$

Question Number 155643 Answers: 0 Comments: 1

Question Number 155642 Answers: 0 Comments: 3

Question Number 155639 Answers: 1 Comments: 4

Question Number 155638 Answers: 1 Comments: 2

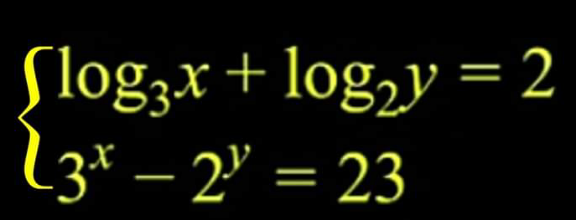
Question Number 155631 Answers: 2 Comments: 2

(x+3(x−2)=x+10

$(x + 3 (x - 2) = x + 10$

Question Number 155630 Answers: 1 Comments: 0

Question Number 155628 Answers: 1 Comments: 0

Pg 568 Pg 569 Pg 570 Pg 571 Pg 572 Pg 573 Pg 574 Pg 575 Pg 576 Pg 577

Contact: info@tinkutara.com