
Question and Answers Forum
AllQuestion and Answers: Page 581


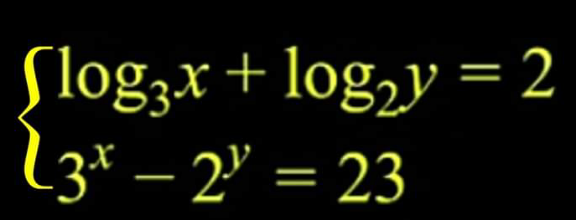










Pg 576 Pg 577 Pg 578 Pg 579 Pg 580 Pg 581 Pg 582 Pg 583 Pg 584 Pg 585
|
Question and Answers Forum |
AllQuestion and Answers: Page 581 |

|

|
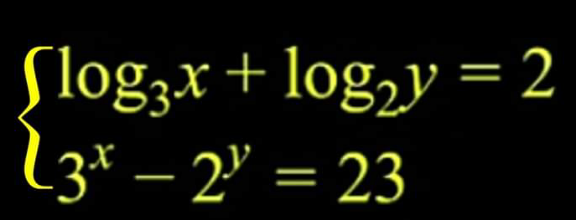
|
| (x+3(x−2)=x+10 |

|

|
| lim_(x→0) (((tanx)/x))^(1/x^2 ) = ? |

|
| Find: 𝛀 = lim_(x→1) ((∫_(x-1) ^(e^x -e) cos(t^5 )dt)/(3^x - 3)) = ? |
| 𝛀 =∫_( 0) ^( 1) (x^(49) /(1 + x + x^2 + x^3 ... x^(100) )) dx = ? |
| if x;y∈R and x^3 +y^3 =16 prove that: x^4 + y^4 + 2x^2 + y^2 ≥ 4x + 36 |

|

|
| How to proof f:X→Y f is 1 to 1 ⇐⇒ f(E)\f(F)=f(E\F) |
| Evaluate the limit and prove by the ε−δ definition that as n→∞ for z≥1 (2(z)^(1/n) − 1)^n → z^2 |

|
| the polynomial 4x^3 +ax^2 +bx+9, where a and b consant, is denoted by f(x). when f(x) is divide by (x−2) the remainder is r and when divided by (x−3) the remaider is 6r. its further given that (x+3) is a factor of f(x). Show that b−a=14 and hence find a and b |
| The mean and standard deviation of 20 observation are found to be 10 and 2 respectively .On rechecking it was found that an observation 8 was incorrect.Calculate the incorrect mean and standard deviation (a)If the wrong iterm was ommited (b) If it is replaced by 12 |

|
| Find Z^4 =1. Hence show that 1+w+w^2 +w^3 =0 |
| Find the cube root of one .Hence show that the sum of the root is equal to zero |
| for a,b,c,d,e ∈R and a+b+c+d+e=5 find the minimum value of a^2 +2b^2 +3c^2 +4d^2 +5e^2 =? |

|

|

|
| ∫_(−∞) ^( ∞) ((sin(x^2 )cos(x^3 ))/((ln((sin(x)cos(x))^2 ))^2 +1)) dx |
Pg 576 Pg 577 Pg 578 Pg 579 Pg 580 Pg 581 Pg 582 Pg 583 Pg 584 Pg 585 |