
Question and Answers Forum
AllQuestion and Answers: Page 601



Pg 596 Pg 597 Pg 598 Pg 599 Pg 600 Pg 601 Pg 602 Pg 603 Pg 604 Pg 605
|
Question and Answers Forum |
AllQuestion and Answers: Page 601 |
| solve in x∈C sin x=(3/2) |
| define d(n) to be the sum of the digits of n. i.e d(1000) = 1 , d(999) = 27 find d(d(d(d(d(5^(10^(100) ) ))))) |
| ∫ (1/(1+(√(2x)) )) dx =? |
| Ω := ∫_0 ^( (π/2)) cos(2x).ln(sin(x))dx=^? −(π/4) solution (1 ) Ω := ∫_0 ^( (π/2)) ( 2cos^( 2) (x)−1)ln(sin(x))dx := 2∫_0 ^( (π/2)) cos^( 2) (x).ln(sin(x))dx−∫_0 ^( (π/2)) ln(sin(x))dx we know that : ∫_0 ^(π/2) ln(sin(x))dx=_(earlier) ^(derived) ((−π)/2) ln(2) ∫_0 ^( (π/2)) cos^( 2) (x).ln(sin(x))dx=_(posts) ^(previous) −(π/4)ln(2)−(π/8) ∴ Ω := −(π/2) ln(2) −(π/4) +(π/2) ln(2) ◂ Ω =− (π/4) ▶ m.n |
| sin(9) + sin(21)+sin(39)=^? (ϕ/( (√2))) ϕ:= golden ratio m.n |
| y′′′+y′=sec x |

|
| find ∫((√(x^2 −9))/x^3 ) dx=? |
| sin(sin(sin(x^(2πx) −1))) = cos(cos(cos(x^(2ex) +1))) x = ? |
| Show whether Σ_(n = 1) ^∞ ((x^2 /(3 + n^2 x^2 ))) is uniformly convegence for real value of x. |
| L=lim_(x→1) (((√(2019x−2018))−1)/( (x^(2019) )^(1/(2018)) −1)) then 2×L =? |
| ((x/5) + (y/3))((5/x) + (3/y)) = 139, ∀x,y ∈ R_(>0) find maximum and minimum of ((x + y)/( (√(xy)))) |
| a,b,c ∈ Z ∣a−b∣^3 + ∣b−c∣^3 = 1 Find the value of ∣a−b∣ + ∣b−c∣ + ∣c−a∣ |
|
| Evaluate the line integral space if f(r)=Zi+Xj+Yk and C is a helix given by C: r(t)=(cost,sint,−3t) 0≤t≤2π |
| my notifications dont work. am i the only one with this problem? how can i contact tinku tara and do they still update the app? |
|
|
| Find area of region that satisfy ∣x−2∣ + ∣y+3∣ < 3 |
| 2016−2x = ∣x−a∣+∣x−b∣+∣x−c∣ has only one solution . a<b<c a,b,c ∈ Z Find the lowest value of c. |

|

|

|
| Given a set consisting of 22 integer A={±a_1 ,±a_2 ,...,±a_(11) }. Show that exist subset of S with properties (1) for every i=1,2,3,...,11 have least one between a_i or −a_i element of S (2)the sum all possible numbers in S divisible by 2015 |
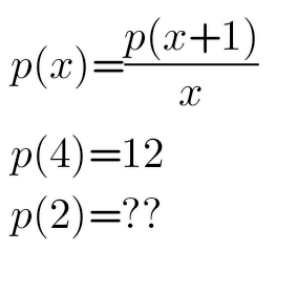
|
| { (((x+1)^2 =x+y+2)),(((y+1)^2 =y+z+2)),(((z+1)^2 =z+x+2)) :} |
Pg 596 Pg 597 Pg 598 Pg 599 Pg 600 Pg 601 Pg 602 Pg 603 Pg 604 Pg 605 |