
Question and Answers Forum
AllQuestion and Answers: Page 676

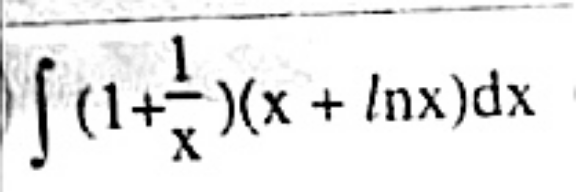


Pg 671 Pg 672 Pg 673 Pg 674 Pg 675 Pg 676 Pg 677 Pg 678 Pg 679 Pg 680
|
Question and Answers Forum |
AllQuestion and Answers: Page 676 |
| Solve the equation: 2^a 3^b 7^c = c^2 cbb^6 ^(−) ; a;b;c∈P |
| Find the last digit of the number: 1^(1989) +2^(1989) +3^(1989) +...+1989^(1989) |
| If F(x+1)=F(x−1)=x^2 then F^(−1) (x)=? |
| cos^2 1°+cos^2 2°+cos^2 3°+...+cos^2 360° = ? |
| ∫_0 ^1 ((ln(1+x)ln(1+x^2 ))/x)dx=(π/2)G−((33)/(32))ζ(3) |

|
| Find the maximum distance between two points on the curve (x^4 /a^4 ) + (y^4 /b^4 ) = 1 . |
| lcm(2a;3a)=lcm(45;100)⇒a=? |
| ∫ (((2+(√x)))/((x+1+(√x))^2 )) dx =? |
| Σ_(k=1) ^(35) ((√k)/(k + (√(k^2 + k)))) = ? |
| exercise Let a and b be natural integers such that 0<a<b. 1. Show that if a divides b, then for any naturel number n, n^a −1 divides n^b −1. 2. For any non−zero naturel number n, prove that the remainder of the euclidean division of n^b −1 by n^a −1 is n^r −1 where r is the remainder of the euclidean division of b by a. 3. For any non−zero naturel number n, show that gcd(n^b −1, n^a −1) = n^d −1 where d = gcd(b,c). by professor henderson^(−) . |
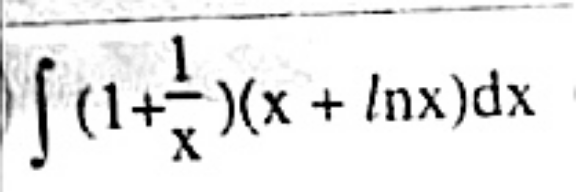
|

|
| x∈Z^+ 15^(48a+1) ≡ x (mod 17) find x=? |
| Let a,b > 0 and a+b+1 = 3ab. Prove that (1) (a^2 /(a+1))+(b^2 /(b+1)) ≥ (a/(a^2 +1))+(b/(b^2 +1)) (2) (a^2 /(b+1))+(b^2 /(a+1)) ≥ (a/(b^2 +1))+(b/(a^2 +1)) |
| Π_(k=1) ^(12) 2∙sin(((πk)/(24))) = ? |
| 𝛗 := ∫_( 0) ^( (π/2)) ((( x)/(cot ( x ))) )^( 3) dx=? |
| resoudre I=∫_0 ^(π/2) tan(nx)tan^n (x)dx |

|
| solve (d^2 x/dt^2 )=cosx |
| find the value lim_(n→∞) (1+((1+(1/2)+(1/3)+(1/4)+...+(1/n))/n^2 ))^n |
| Σ_(n≥0) (((−1)^n )/((n+z)n!)) |
| ∫_0 ^∞ x^n (e^(ix) )^z dx=??? (z∈C) |
| Σ_(n=1) ^∞ (((2n)!!)/(2^n ∙(n+1)∙(2n+1)!!))=? |
| S(x)=Σ_(n=1) ^∞ (((2n)!!)/((2n+1)!!))x^(2n) =?........(∣x∣<1) |
| if z^2 - 16(√z) = 12 find z - 2(√z) = ? |
Pg 671 Pg 672 Pg 673 Pg 674 Pg 675 Pg 676 Pg 677 Pg 678 Pg 679 Pg 680 |