
Question and Answers Forum
AllQuestion and Answers: Page 708




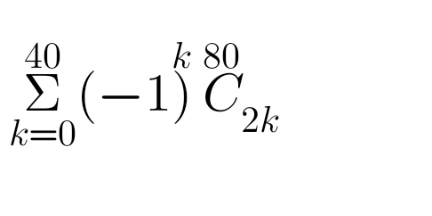


Pg 703 Pg 704 Pg 705 Pg 706 Pg 707 Pg 708 Pg 709 Pg 710 Pg 711 Pg 712
|
Question and Answers Forum |
AllQuestion and Answers: Page 708 |

|
| ∫_0 ^∞ ((sinx)/x^μ )dx =? |
| Given that a ≥ 1 ≥ b > 0. Prove the followings: (1) (1/2)(a−b)^2 ≤ (a−1)^2 +(1−b)^2 ≤ (a−b)^2 (2) (1/4)(a−b)^3 ≤ (a−1)^3 +(1−b)^3 ≤ (a−b)^3 |
| Σ_(n=0) ^∞ ((ζ(2n+2)(−1)^n )/4^n )=? |
| (((4−(√(15))))^(1/6) /( (√(4−(√(15)))) ∙ ((4+(√(15))))^(1/3) )) = ? |
| Nice...≽≽≽∗∗∗≼≼≼...Calculus Ω:=∫_0 ^( 1) (((1−(x)^(1/3) )(1−((x ))^(1/5) )(1−(x)^(1/7) ))/(ln( ((x ))^(1/3) ))) dx=? ....m.n |

|
| lim_(x→∞) (((x!)/x^x ))^(1/x) |

|
| Show that for n∈ N, A_n =n^2 (n^2 −1) is divisible by 12 |
| lim_(x→0^+ ) ((x^((sin x)^x ) −(sin x)^x^(sin x) )/x^3 )=? |
| lim_(x→0) ((lnlnln[x+(1+x)^(((1+x)^(1/x) )/x) ]+x(1−(1/e^(e+1) )))/x^2 )=? |

|
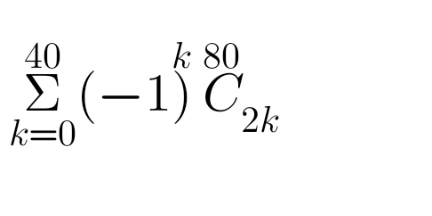
|

|
| lim_(x→0) (((e^(sin x) +sin x)^(1/(sin x)) −(e^(tan x) +tan x)^(1/(tan x)) )/x^3 )=? |

|
| evaluate: Θ:=Σ_(n=1) ^∞ ((ζ(n+1)−1)/(n+1)) =? |
| L(((1+2bt)/( (√t)))e^(bt) )(s)=? |
| Three interior angles of a polygon are 160° each. If the other interior angles are 120° each, find the number of sides of the polygon. |
| lim_(x→0) ((tan (tan x)−tan (tan (tan x)))/(tan x∙tan (tan x)∙tan (tan (tan x))))=? |

|
| lim_(x→0) ((1−e^(sin x ln (cos x)) )/x^3 ) =? |
| ∫_0 ^( 2) (√(1+e^(2x) ))dx |
| .......Advanced ...∗∗∗∗∗ ...Integral...... Prove that :: Φ :=∫_0 ^( 1) ((1−x)/((1−x+x^2 )log(x)))dx= proof:: Φ:=∫_0 ^( 1) ((1−x^2 )/((1−x^3 )log(x)))dx f (a):= ∫_0 ^( 1) ((1−x^a )/((1−x^3 )log(x))) Φ := f (2) ........✓ f ′(a):=∫_0 ^( 1) ((−x^a log(x))/((1−x^3 )log(x)))=∫_0 ^( 1) ((−x^a )/(1−x^3 ))dx (★) (★):: x^3 =y ⇒ f ′(a):=(1/3)∫_0 ^( 1) ((y^((−2)/3) −y^((a/3)−(2/3)) )/(1−y))dy :=(1/3)∫_0 ^( 1) ((y^((−2)/3) −1+1−y^((a/3)−(1/3)) )/(1−y))dy :=(1/3)(ψ((a/3)+(2/3))−ψ((2/3))) f (a):=log(Γ((a/3)+(2/3)))−(a/3)ψ((2/3))+C f (0):=0=log(Γ((2/3)))+C C :=−log(Γ((2/3))) Φ:= f (2)=log(Γ((4/3)))−(2/3) ψ((2/3))−log(Γ((2/3))) :=log(((Γ((4/3)))/(Γ((2/3)))))−(2/3)ψ((2/3)) ....✓ |
| ∫_(1/3) ^3 ((x+sin (x^2 −(1/x^2 )))/(x(2+cos (x+(1/x))))) dx ? |
Pg 703 Pg 704 Pg 705 Pg 706 Pg 707 Pg 708 Pg 709 Pg 710 Pg 711 Pg 712 |