
Question and Answers Forum
AllQuestion and Answers: Page 743









Pg 738 Pg 739 Pg 740 Pg 741 Pg 742 Pg 743 Pg 744 Pg 745 Pg 746 Pg 747
|
Question and Answers Forum |
AllQuestion and Answers: Page 743 |
| show that ∫_0 ^( ∞) ((cos((√x)))/(e^(2π(√x)) −1))dx = 1−(e/((e−1)^2 )) |
| If tan 14° = x then tan 18° =? |
| find the first root (−8i)^(1/2) |

|

|

|
| L=lim_(x→0) ((6sin(sin(sin(sinx)))−6x+5x^3 )/x^5 ) |
| Given f(x)=(√(2+x^2 −x)) +(√(2−x^2 )) If (g○f)(x) = 2x+1 then g^(−1) (−1)=? |
| If a, b and c are integers not all simultaneously equal and w≠1 is a cube root of unity, then the minimum value of ∣a+bw+cw^2 ∣ is (A) 0 (B) 1 (C) (√3)/2 (D) 1/2 |
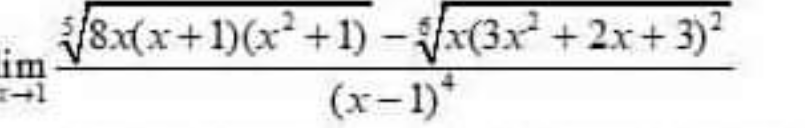
|

|
| Bug in version 2.265 1. the cursor keys ↑↓ seem not to work. 2. when inserting new lines with Enter key, the cursor doesn′t move. |

|
| Solve for real number(((x−1)^2 )/2)+(((y−2)^2 )/4)+(((z−3)^2 )/6)+3=∣x−1∣+∣y−2∣+∣z−3∣ |
| Near the shore a fisherman jumps out of his boat with a velocity of 5.00 ms^(−1) and lands on the shore 0.650 afterwards.The boat moves backwards. The respective masses of the fisherman and the boat are 85.0 kg and 165 kg and the frictional force between the boat and water is negligible. What will be the distance between the fisherman and the both at the instant when he just lands on the shore? |
| Σ_(n_1 +2n_2 +3n_3 +..+rn_r =n) ^n (1/(n_1 !n_2 !n_3 !..n_r !1^n_1 2^n_2 3^n_3 4^n_4 ...r^n_r ))=1 0≥n_1 ,n_2 ,n_3 ,..≥n Prove the above identity |
| ........ advanced ... ... ... calculus........ Φ= lim_(n→∞) {∫_1 ^( n) (x/([x]^2 )) dx −ψ(n+1)}=? solution: Φ_n =∫_1 ^( n) (x/([x]^2 )) dx=Σ_(k=1) ^(n−1) ∫_k ^( k+1) (x/k^2 ) dx = (1/2)Σ_(k=1) ^(n−1) (1/k^2 )(2k+1)=Σ_(k=1) ^(n−1) (1/k)+(1/2)Σ_(k=1) ^(n−1) (1/k^2 ) Φ = lim_(n→∞) (Φ_n −ψ(n+1)) = (π^2 /(12)) +lim_(n→∞) (Σ_(k=1) ^(n−1) (1/k)−ψ(n+1)) =_(2 : ψ(n+1)= H_n −γ ) ^(1 :ψ (n+1) := (1/n) +ψ(n)) (π^2 /(12))+lim_(n→∞) (Σ_(k=1) ^(n−1) (1/k)−H_n +γ) ∴ Φ := (π^2 /(12)) +γ −lim_(n→∞) ((1/n)) ......... Φ:=(1/2) ζ (2) +γ γ :: Euler− Mascheroni constant... |
| Π_(i=0) ^5 (1−cotan(20+i)) =^? 8 |

|

|

|
| (1/3) − ((x−3)/9) + (((x−3)^2 )/(27)) + ... =? |
| .......advanced calculus...... prove that:: lim_(n→∞) {(((−1)^(n+1) n^(n+1) )/(n!)) (d^( n) /dx^n )(((ln(x))/x))∣_(x=n) }=γ γ : euler −mascheroni constant |

|
| ......advanced calculus..... prove that: i::𝛗=∫_0 ^( ∞) ((1/2)e^(−2x) −(1/(1+e^x )))(1/x) dx=log((1/( (√π))) ) ii::∫_0 ^( ∞) ((1/2)−(1/(1+e^(−x) )))(e^(−2x) /x)dx=log(((√π)/2)) |
| lim_(x→0) ((x^n sin^n x)/(x^n −sin^n x)) is non-zero finite, then find n? |
Pg 738 Pg 739 Pg 740 Pg 741 Pg 742 Pg 743 Pg 744 Pg 745 Pg 746 Pg 747 |