Question and Answers Forum
Question Number 108766 by bemath last updated on 19/Aug/20
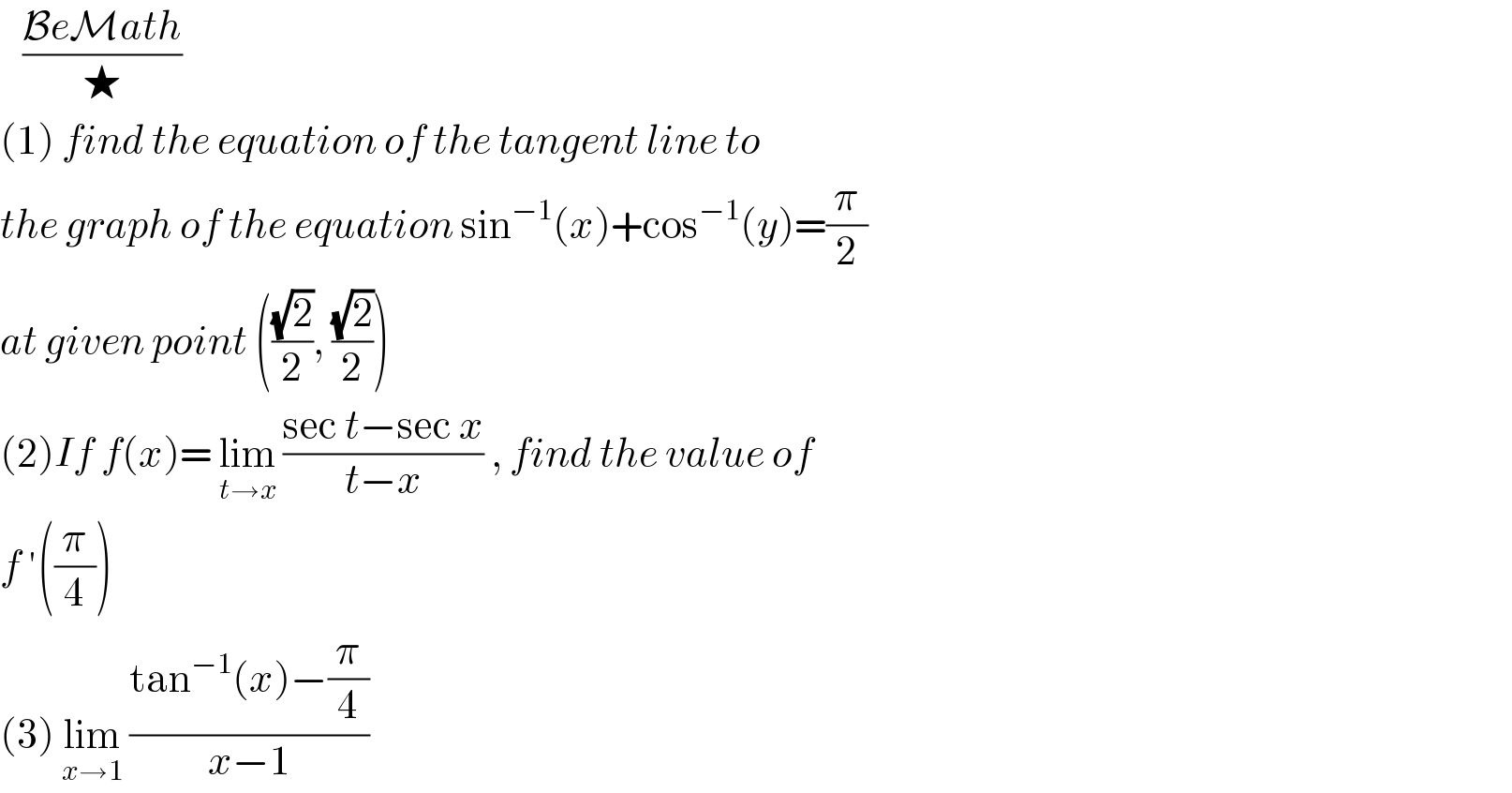
Answered by Dwaipayan Shikari last updated on 19/Aug/20
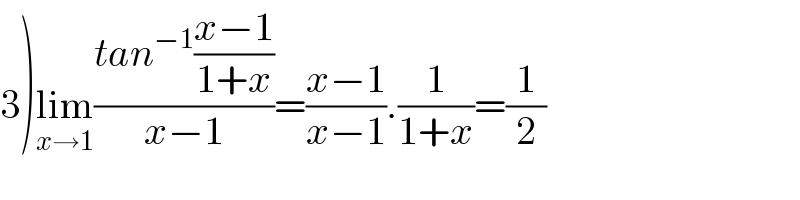
Answered by john santu last updated on 19/Aug/20
![((⊸JS⊸)/♥) (1) (d/dx) [ sin^(−1) (x)+cos^(−1) (y) ] = 0 ⇒(1/( (√(1−x^2 )))) −(1/( (√(1−y^2 )))) y′(x) = 0 gradient ⇒y′(((√2)/2)) = ((√(1−(1/2)))/( (√(1−(1/2))))) = 1 ∴ the equation of tangent line y = 1.(x−((√2)/2))+((√2)/2) ; y = x (2)f(x) = lim_(t→x) ((sec t−sec x)/(t−x)) ⇒f(x) = lim_(t→x) ((cos x−cos t)/(cos t.cos x (t−x))) ⇒f(x) = lim_(t→x) (1/(cos t.cos x)) . lim_(t→x) ((−2sin (((x+t)/2))sin (((x−t)/2)))/(t−x)) ⇒f(x) = ((sin x)/(cos^2 x)) →f ′(x) = ((cos^3 x+2sin^2 x cos x)/(cos^4 x)) ⇒f ′(x) = ((cos^2 x+2sin^2 x)/(cos^3 x)) therefore f ′((π/4)) = (((1/2)+2.(1/2))/(1/(2(√2)))) = (3/2). 2(√2) = 3(√2) (3) lim_(x→1) ((tan^(−1) (x)−(π/4))/(x−1)) = lim_(x→1) [ (1/(1+x^2 )) ] =(1/2)](Q108767.png)
Commented by bemath last updated on 19/Aug/20

Answered by mathmax by abdo last updated on 19/Aug/20
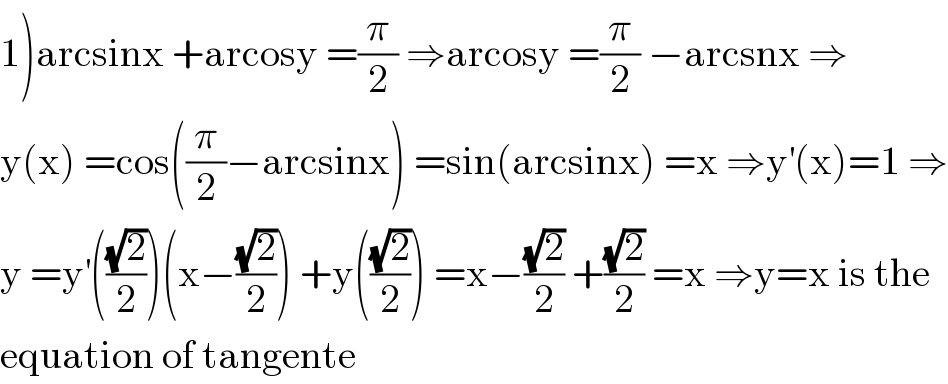
Answered by mathmax by abdo last updated on 19/Aug/20
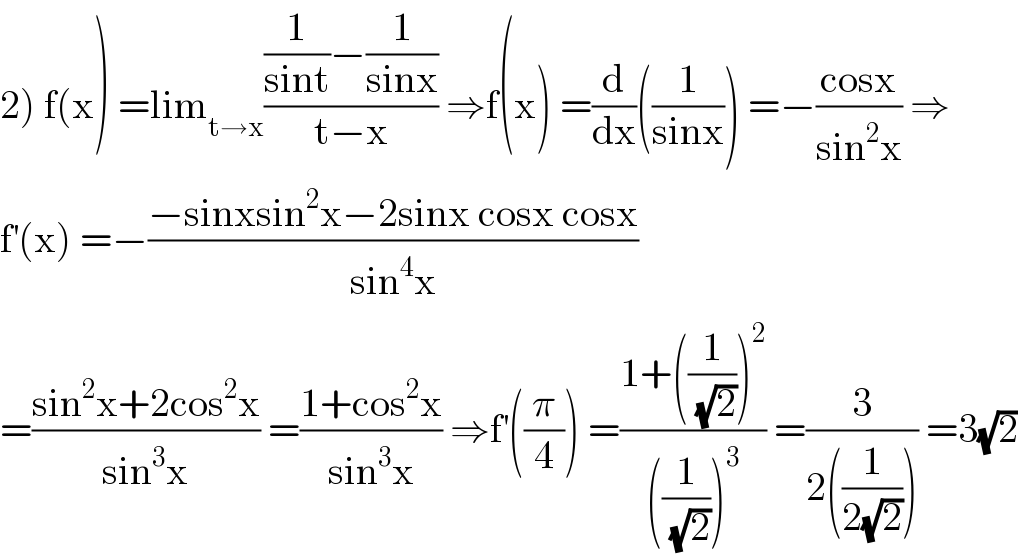
Answered by mathmax by abdo last updated on 19/Aug/20