
Question and Answers Forum
Question Number 138703 by mathocean1 last updated on 16/Apr/21
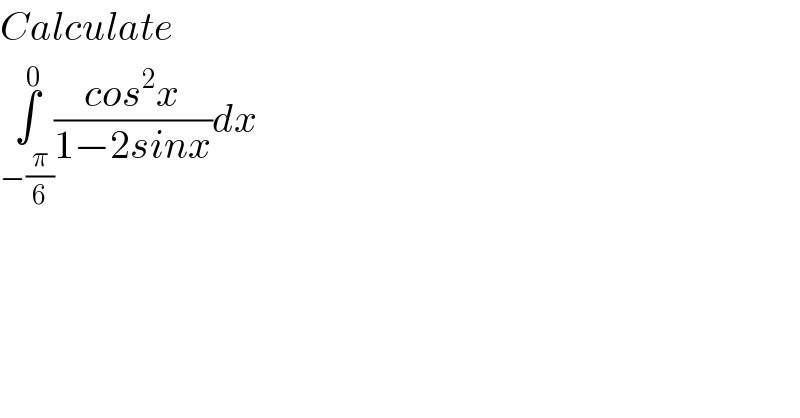
Commented by SanyamJoshi last updated on 17/Apr/21

Answered by Mathspace last updated on 16/Apr/21
![I=∫_(−(π/6)) ^0 ((cos^2 x)/(1−2sinx))dx =_(x=−t) ∫_0 ^(π/6) ((cos^2 t)/(1+2sint))dt =∫_0 ^(π/6) ((1−sin^2 t)/(1+2sint))dt we have ((1−x^2 )/(2x+1))=−(1/4)((4x^2 −4)/(2x+1)) =−(1/4)(((4x^2 −1)/(2x+1))−(3/(2x+1))) =−(1/4)(2x−1)+(3/(4(2x+1))) ⇒ I=−(1/4)∫_0 ^(π/6) (2sint−1)dt +(3/4)∫_0 ^(π/6) (dt/(2sint +1))(=J) =−(1/2)[−cost]_0 ^(π/6) +(1/4).(π/6) +(3/4)J =−(1/2)(1−((√3)/2))+(π/(24))+(3/4)J J=∫_0 ^(π/6) (dt/(2sint +1)) =_(tan((t/2))=y) ∫_0 ^(2−(√3)) ((2dy)/((1+y^2 )(2((2y)/(1+y^2 ))+1))) =2∫_0 ^(2−(√3)) (dy/(4y+y^2 +1)) =2∫_0 ^(2−(√3)) (dy/(y^2 +4y+1)) Δ^′ =2^2 −1=3 ⇒y_1 =−2+(√3) y_2 =−2−(√3) ⇒ 2∫_0 ^(2−(√3)) (dy/((y−y_1 )(y−y_2 ))) =2(1/(2(√3)))∫_0 ^(2−(√3)) ((1/(y−y_1 ))−(1/(y−y_2 )))dy =(1/( (√3)))[log∣((y+2−(√3))/(y+2+(√3)))∣]_0 ^(2−(√3)) =(1/( (√3))){log(((4−2(√3))/4))−log(((2−(√3))/(2+(√3))))} I=−(1/2)+((√3)/4)+(π/(24))+((√3)/4){log(1−((√3)/2))−log(((2−(√3))/(2+(√3))))}](Q138705.png)
| ||
Question and Answers Forum | ||
Question Number 138703 by mathocean1 last updated on 16/Apr/21 | ||
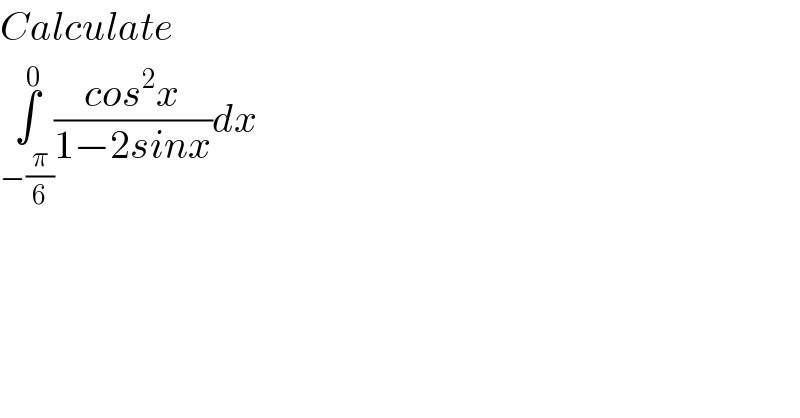 | ||
Commented by SanyamJoshi last updated on 17/Apr/21 | ||
 | ||
Answered by Mathspace last updated on 16/Apr/21 | ||
![I=∫_(−(π/6)) ^0 ((cos^2 x)/(1−2sinx))dx =_(x=−t) ∫_0 ^(π/6) ((cos^2 t)/(1+2sint))dt =∫_0 ^(π/6) ((1−sin^2 t)/(1+2sint))dt we have ((1−x^2 )/(2x+1))=−(1/4)((4x^2 −4)/(2x+1)) =−(1/4)(((4x^2 −1)/(2x+1))−(3/(2x+1))) =−(1/4)(2x−1)+(3/(4(2x+1))) ⇒ I=−(1/4)∫_0 ^(π/6) (2sint−1)dt +(3/4)∫_0 ^(π/6) (dt/(2sint +1))(=J) =−(1/2)[−cost]_0 ^(π/6) +(1/4).(π/6) +(3/4)J =−(1/2)(1−((√3)/2))+(π/(24))+(3/4)J J=∫_0 ^(π/6) (dt/(2sint +1)) =_(tan((t/2))=y) ∫_0 ^(2−(√3)) ((2dy)/((1+y^2 )(2((2y)/(1+y^2 ))+1))) =2∫_0 ^(2−(√3)) (dy/(4y+y^2 +1)) =2∫_0 ^(2−(√3)) (dy/(y^2 +4y+1)) Δ^′ =2^2 −1=3 ⇒y_1 =−2+(√3) y_2 =−2−(√3) ⇒ 2∫_0 ^(2−(√3)) (dy/((y−y_1 )(y−y_2 ))) =2(1/(2(√3)))∫_0 ^(2−(√3)) ((1/(y−y_1 ))−(1/(y−y_2 )))dy =(1/( (√3)))[log∣((y+2−(√3))/(y+2+(√3)))∣]_0 ^(2−(√3)) =(1/( (√3))){log(((4−2(√3))/4))−log(((2−(√3))/(2+(√3))))} I=−(1/2)+((√3)/4)+(π/(24))+((√3)/4){log(1−((√3)/2))−log(((2−(√3))/(2+(√3))))}](Q138705.png) | ||
| ||