
Question and Answers Forum
Coordinate GeometryQuestion and Answers: Page 7















|
Question and Answers Forum |
Coordinate GeometryQuestion and Answers: Page 7 |

|

|
| Find the area of the triangle in the first quadrant between the x and y axis and the tangent to the relationship curve y=(5/x)−(x/5) and x dont equal 0 at (0,5) |
| Donnes: AD=1; DB=6; ∡BCD=45° ; ∡BAC=90° Determiner 1) AC ? 2) AE? −−−−−−−−−−−− Solution △BAC ∡BAC=90° BC^2 =AB^2 +AC^2 CD (cote commun aux △BAC et BDC) DB^2 =CD^2 +BC^2 −2BC×CDcos 45° (1) △CAD CD^2 =AD^2 +AC^2 (1) DB^2 =(AD^2 +AC^2 )+(AB^2 +AC^2 )−2(√((AB^2 +AC^2 )(AD^2 +AC^2 ))) cos 45° DB^2 =(AD^2 +AB^2 +2AC^2 −(√(2(AB^2 +AC^2 )(AD^2 +AC^2 ))) 2(AB^2 +AC^2 )(AD^2 +AC^2 )=(AD^2 +AB^2 +2AC^2 −DB^2 )^2 posons: AC=x 2(49+x^2 )(1+x^2 )=(1+49+2x^2 −36)^2 (x^4 +50x^2 +49)=2(x^4 +14x^2 +49) x^4 −22x^2 +49=0 x^2 =11±6(√2) x=(√(11+6(√2) )) AC =4,4142135 2)AB et AC coupent le cercle en (D,B) et( E,C) Nous avons AD×AB=AE×AC AE=((AD×AB)/(AC))=(7/( (√(11+6(√2)))))=((7(√(11+6(√2))))/(11+6(√2))) AE=1,585786 |

|

|

|

|

|

|

|

|

|

|

|

|
| The equations of the sides AC, BC and AB of a right−angled triangled with lengths a, b and c are y = −7, x=11 and 4x−3y−5=0 respectively. Find the equation of the inscribed circle of the triangle, if its radius r, is given by r = ((a+b−c)/2). |

|

|

|
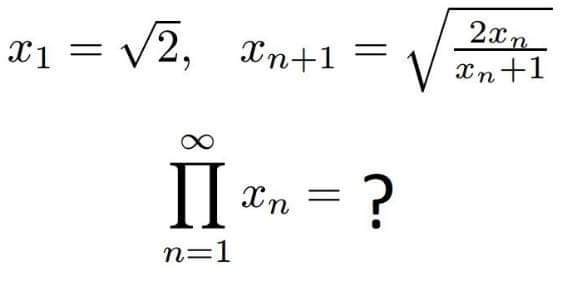
|
| Dterminer la valeur de x |

|

|

|

|