
Question and Answers Forum
Question Number 9306 by tawakalitu last updated on 29/Nov/16
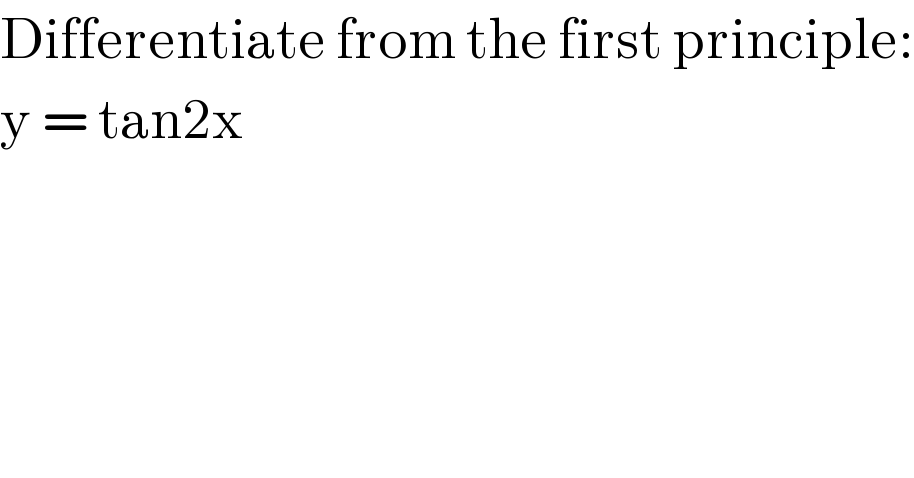
Answered by mrW last updated on 30/Nov/16
![y(x)=tan (2x) y(x+h)=tan (2x+2h)=((tan (2x)+tan (2h))/(1−tan (2x)×tan (2h))) y(x+h)−y(x)=((tan (2x)+tan (2h))/(1−tan (2x)×tan (2h)))−tan (2x) =((tan (2x)+tan (2h)−tan (2x)+tan^2 (2x)×tan (2h))/(1−tan (2x)×tan (2h))) =((1+tan^2 (2x))/((1/(tan (2h)))−tan (2x))) ((y(x+h)−y(x))/h)=((1+tan^2 (2x))/((h/(tan (2h)))−tan (2x)×h)) lim_(h→0) (h/(tan (2h)))=lim_(h→0) (1/(2×((tan (2h))/(2h))))=(1/2) lim_(h→0) tan (2x)×h=0 (dy/dx)=lim_(h→0) ((y(x+h)−y(x))/h)=((1+tan^2 (2x))/(1/2))=2[1+tan^2 (2x)]=(2/(cos^2 (2x)))](Q9308.png)
Commented by tawakalitu last updated on 29/Nov/16

| ||
Question and Answers Forum | ||
Question Number 9306 by tawakalitu last updated on 29/Nov/16 | ||
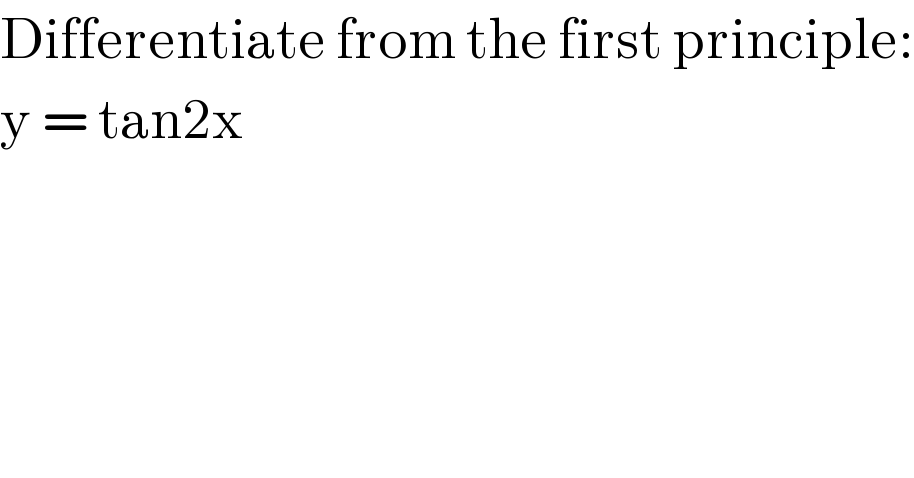 | ||
Answered by mrW last updated on 30/Nov/16 | ||
![y(x)=tan (2x) y(x+h)=tan (2x+2h)=((tan (2x)+tan (2h))/(1−tan (2x)×tan (2h))) y(x+h)−y(x)=((tan (2x)+tan (2h))/(1−tan (2x)×tan (2h)))−tan (2x) =((tan (2x)+tan (2h)−tan (2x)+tan^2 (2x)×tan (2h))/(1−tan (2x)×tan (2h))) =((1+tan^2 (2x))/((1/(tan (2h)))−tan (2x))) ((y(x+h)−y(x))/h)=((1+tan^2 (2x))/((h/(tan (2h)))−tan (2x)×h)) lim_(h→0) (h/(tan (2h)))=lim_(h→0) (1/(2×((tan (2h))/(2h))))=(1/2) lim_(h→0) tan (2x)×h=0 (dy/dx)=lim_(h→0) ((y(x+h)−y(x))/h)=((1+tan^2 (2x))/(1/2))=2[1+tan^2 (2x)]=(2/(cos^2 (2x)))](Q9308.png) | ||
| ||
Commented by tawakalitu last updated on 29/Nov/16 | ||
 | ||