
Question and Answers Forum
DifferentiationQuestion and Answers: Page 12
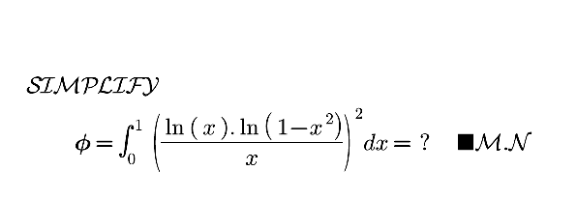

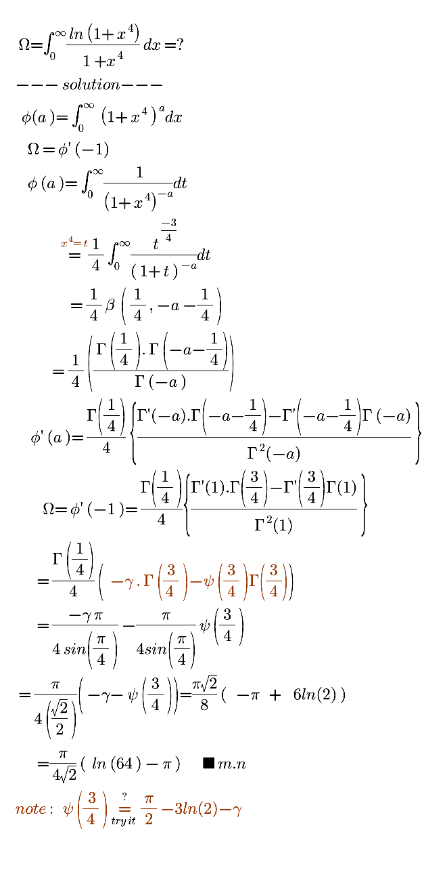




|
Question and Answers Forum |
DifferentiationQuestion and Answers: Page 12 |
| Ω = ∫ sin^( 2) (x).cos^( 4) (x ) dx |
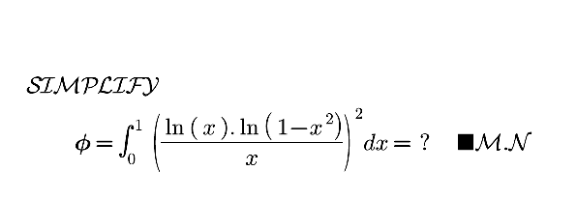
|
| y = (√x) Find (dy/dx) by first principle. |
| differenciate using implicit function 2x+4y+sin xy=3 |
| calculate Ω = Σ_(n=1) ^∞ (( (−1)^( n) n)/(3^( n) (2n −1 ))) =? − Inspired from Sir Ghaderi′s post− |

|
| prove that ψ′′ ((1/4) )= −2π^( 3) − 56 ζ (3 ) |
| If x ∈R the maximum value of ((3x^2 +9x+17)/(3x^2 +9x+7)) is ... |
| lim_( n→∞) ((1/(1+n^( 3) )) +(( 4)/(8 +n^( 3) )) + (9/(27 +n^( 3) )) +...+(n^( 2) /(2n^( 3) )) )=? |
| Solve the integro−differential equation: i(t) + 4(di/dt) + ∫i(t)dt = 2 cos (3t+ 60°) where i(t) is a sinulsodial current. |
| write the taylor expansion of : f(x)= x^( 2) . cos(x) at x=1 then f^( (5 )) (x) at x=1 ? |
| prove that.... ( 1+ (1/n) )^( n) < e < (1+(1/n) )^( n+1) |
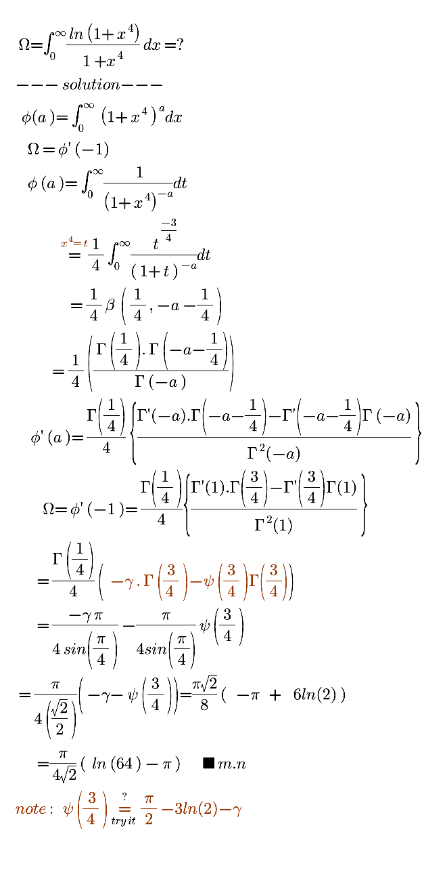
|

|
| differenciate xsin xcos x |
| f (x ) = cos^( 2) ( x ) + sin^( 4) ( x ) R_( f) = ? −−−solution−−− y = cos^( 2) (x ) + sin^( 2) (x) .( 1−cos^( 2) (x)) = 1 − (1/4) sin^( 2) ( 2x) we know that : 0≤ sin^( 2) ( αx) ≤1 therefore −1≤− sin^( 2) (2x) ≤ 0 1−(1/4) ≤ 1− (1/4) sin^( 2) (2x) ≤1 R_( f) = [ (3/4) , 1 ] ◂ ★ ▶ |
| Determine the value of the following proposition . ( True or False ) ∃ x ∈ R ; determinant ((( 1+2x),( 2x),(2x)),(( 2x),( 1+2x),( 2x )),(( 2x),( 2x),(1 +2x)))= x^( 3) + 8x−2 −−−−−−−−− |
| Differentiate y=sin xy |
| Differentiate y=e^(−x^2 ) |
| ≺ X , τ ≻ is a topological space and A ⊆ X , A^− =^? ∩_(F⊃A) F ( F is closed set ) |
| Given P(x) is polynomial such that P(3x)= P ′(x).P ′′(x) . Find the tangent of curve y = P(x) parallel to the line y= 4x−2. |

|

|
| In the given equation below , applying the formula for the derivative of inverse trigonometric functions , what is the ′′u ′′ from the given function. y = cosec^(−1) [ sin (((1+sin x)/(cos x)))] |

|
|