
Question and Answers Forum
DifferentiationQuestion and Answers: Page 14
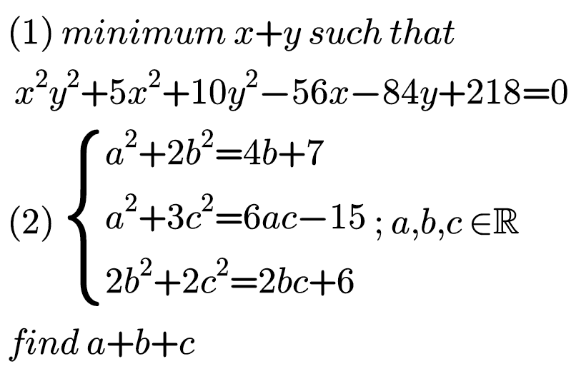
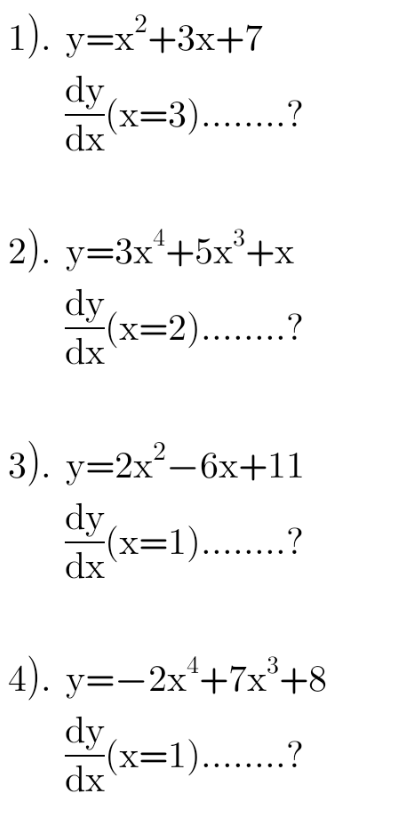





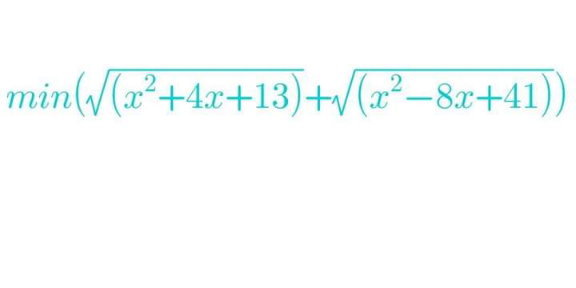
|
Question and Answers Forum |
DifferentiationQuestion and Answers: Page 14 |
| Σ_(n=1) ^∞ (( (−1)^( n) H_( 2n) )/(2n)) =? |
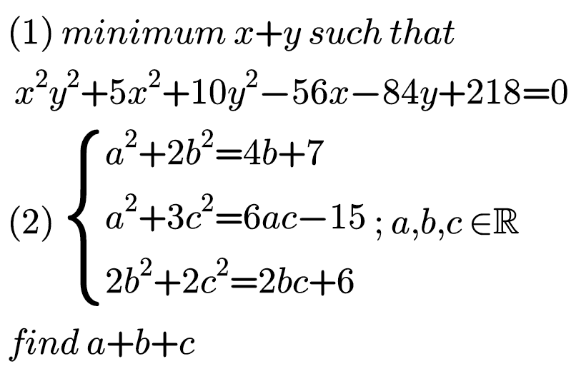
|
| find the partial derivatives of the function with respect to each variable f(x,y)=∫_x ^y g(t) dt |
| prove that: Σ_(n=1) ^∞ tan^( −1) ( (1/F_( n) ) ).tan^( −1) ( (1/F_( n+1) ) )= (π^( 2) /8) Fibonacci numbers |
| question# If , Ω =∫_0 ^( 1) ((ln^( 2) (1−x^( 4) ))/x) dx= a ζ b) find the value of , a , b . |
| Given x,y∈R^+ and ((x/5)+(y/3))((5/x)+(3/y))=139. If maximum and minimum of ((x+y)/( (√(xy)) )) is M and n respectively, then what the value of 3M−4n. |
| EI(∂^4 y/∂x^4 )+ρS(∂^2 y/∂t^2 )=0 (1) y(x,0)=U_0 (x) (∂y/∂t)(x,0)=V_0 (x) ; EI(∂^2 y/∂x^2 )(0,t)=EI(∂^2 y/∂x^2 )(L,t)=0 |
| solve : ( x^( 2) +x −6)^( 3) + (7x^( 2) −9x −2)^( 3) −512(x^2 −x−1)^( 3) =0 x = ? |
| Make tangen line at point (2,3). |
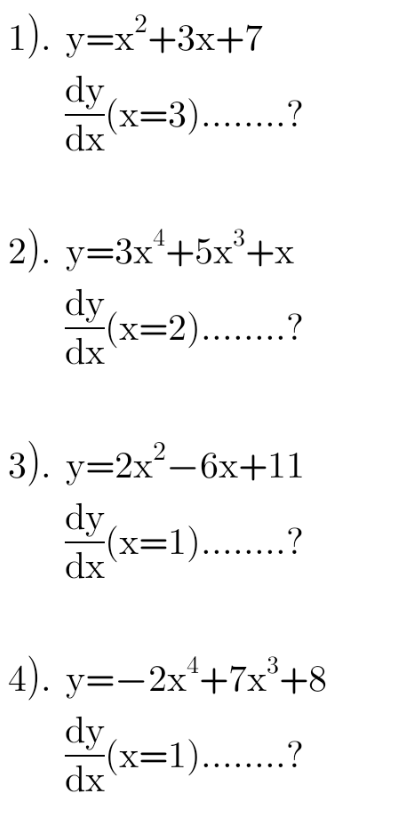
|
| Find derivative of this function 1). f(x)= x.sin x 2). f(x)= e^(5x) . log _2 (3x) 3). f(x)= 3^(3x) .(2x−1) 4). f(x)= ((3x^2 −2)/(4x+1)) |
| f(x)=x^(2014) +2x^(2013) +3x^(2012) +4x^(2011) +...+2014x+2015 min f(x)=? |
| What are the coordinates of the points on the curve x^2 −y^2 =16 which nearest to (0,6)? |

|

|

|
| F(x,y)=x^2 −2xy+6y^2 −12x+2y+45 find x &y such that F(x,y) minimum |

|
| max ∧ min of f(x) =(√x) +4(√((1−x)/2)) |
| φ := ∫_0 ^( 1) (( ln (1−x^( 2) ))/(1+ x^( 2) )) dx = proof : φ = ∫_0 ^( 1) (( ln(1−x ))/(1+x^( 2) ))dx + (π/8)ln(2) .... I= ∫_0 ^( 1) ((ln ( 1−x ))/(1+x^( 2) ))dx =^(x=tan(t)) ∫_0 ^( (π/4)) ln( cos(t)−sin(t))dt−∫_0 ^( (π/4)) ln(cos(t))dt = ∫_0 ^( (π/4)) ln((√2) )dt +∫_0 ^( (π/4)) ln(sin((π/4) −t))dt−(G/2) +(π/4)ln(2) =((3π)/8) ln(2)−(G/2) −(G/2) −(π/4) ln(2)=(π/8)ln(2)−G φ = (π/4)ln(2) − G ■ m.n |
| If x − z = tan^(− 1) (yz) and z = z(x, y), find ((δz)/(δx)) , ((δz)/(δy)) |

|
| find p if y=1−px−3x^2 if the maximum is 13 (help pls) |
| φ (n )= Σ_(k=1) ^n (−1 )^( k−1) ((( n)),(( k)) ) H_( k) Find the value of : Σ_(n=1) ^∞ (−1)^( n−1) φ ( n^( 2) ) =? |
| Ω :=∫_0 ^( 1) (√x) (√(1−(√x) )) (√(1−(√(1−(√x) )))) dx=? |
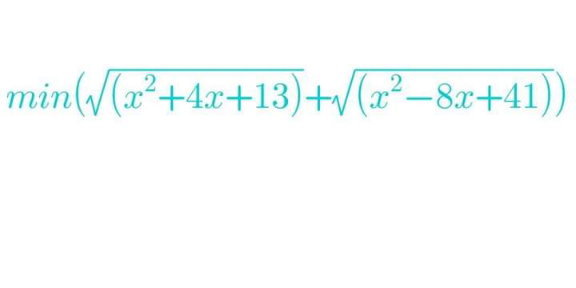
|