
Question and Answers Forum
DifferentiationQuestion and Answers: Page 19






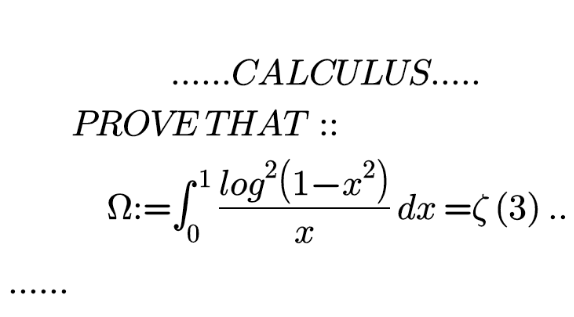

|
Question and Answers Forum |
DifferentiationQuestion and Answers: Page 19 |
| Ω := ∫ ((√(1−sin(x)))/(cos (x))) e^(−(1/2) x) = ? |

|
| Find the shortest distance from the origin to the hyperbola x^2 +8xy+7y^2 =225 ,z=0 |
| A rectangular box,open at the top is to have a volume of 32 cube feet What must be the dimensions so that the total surface is a minimum? |
| If y=cosh (x^2 −3x+1) (d^2 y/dx^2 ) =? |
| ∫ (x−1)h(x)dx = x^3 −sin 2x+(√(x^2 +1)) + c ⇒h ′(1)= ? |
| Evaluate :: 𝛗:=∫_0 ^( ∞) (( sin (x)^(1/( 3 )) )log ((1/x) ))/x)dx=? |
| ......Nice .... Calculus...... Find the value of :: Θ :=Σ_(n =1) ^∞ (1/(4^( n) cos^( 2) ((( π)/( 2^( n + 2) )) ) )) =? .......... |

|
| Find, among all right circular cylinders of fixed volume V that one with smallest surface area (counting the areas of the faces at top and bottom ) |
| The maximum value of y = (√((x−3)^2 +(x^2 −2)^2 ))−(√(x^2 +(x^2 −1)^2 )) is (A) (√(10)) (C) 4 (B) 2(√5) (D) 10 |
| Ω :=∫_(−∞) ^( ∞) ((log(2+x^( 2) ))/(4+x^( 2) ))dx=? |

|
| Prove that:: Ω:=∫_0 ^( 1) ((ln^2 (1−x).ln(x))/x)dx=((−1)/2) ζ (4 ) Without using the “Beta function” m.n |

|

|
| Prove that : ∀n∈N^∗ a. Σ_(k=1) ^n C_n ^k (((−1)^k )/k) = Σ_(k=1) ^n (1/k) b. Σ_(k=1) ^n C_n ^k (((−1)^k )/(2k+1)) = (4^n /((2n+1)C_(2n) ^n )) |
| ........nice .......integral....... T :=∫_0 ^( ∞) ((arctan(x))/x^( ln(x) +1) )dx=^? ((π(√π))/4) |
| ....... nice .....integral....... Evaluate :: ξ := ∫_0 ^( 1) ((ln(1−t))/(1+t^2 )) dt =? |
| .....mathematical ......Analysis.... if :: 𝛗(n):=∫_0 ^( 1) x^(2n−1) log(1+x)dx then find the value of :: Θ:= Σ_(n=1) ^∞ (−1)^n 𝛗(n) .......m.n |
| x^3 =(1/(3!))∫_0 ^x f(x−t)f(t)dt f(x)=? |

|
| Evaluate :: Ω:=∫_0 ^( (π/4)) ((ln(tan(x)).sin^π^e (2x))/((sin^π^e (x)+cos^π^e (x))^2 ))dx |
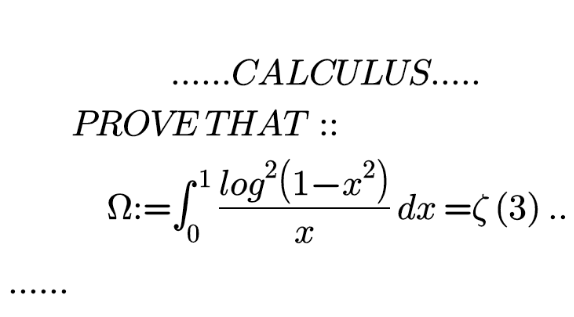
|

|