
Question and Answers Forum
DifferentiationQuestion and Answers: Page 5









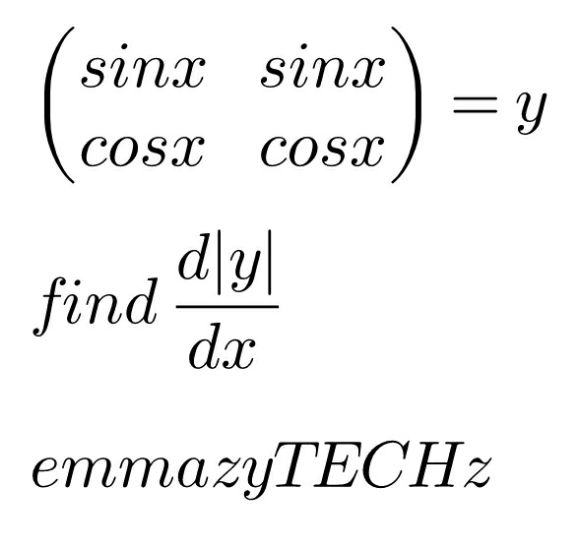
|
Question and Answers Forum |
DifferentiationQuestion and Answers: Page 5 |

|

|
| find the value of the following series . Ω= Σ_(n=1) ^∞ (( cos(((nπ)/4) ))/n^( 2) ) =? |

|
| Given x,y,z>0 and x^2 +y^2 +z^2 +x+2y+3z=23 find maximum of x+y+z. |
| laplace transform −−−−−−− L_t { (( sin(t ))/t) } = F (s ) F (s )= ? then calculate . Ω=∫_0 ^( ∞) ((e^( −2t) sin(t ))/t) dt =? −−−−−−−− |
| F(t)=(4t^3 ,2cos(2t),3e^(3t) ) find F ′(t) F ′(t)=(12t^2 ,-4sin(2t),9e^(3t) ) is my answer correct? |
| Find minimum value of 2x^2 +2xy+4y+5y^2 −x for x and y real numbers |

|

|

|
| determine the value of b for which y=((−x)/3) +b meets the graph of y^2 =x^3 orthogonally |
| find (dy/dx) y=2x^(√x) |
| from first principle y=xInx find (dy/dx) |

|

|

|
| Ω= ∫_0 ^( (π/2)) (( 2sin(x) − cos(x))/(sin(x) + cos (x))) dx = ? −−−− |
| How do you make a curve y=ax^3 +bx^2 +cx+d with a critical point of (1,0) and (−2,27) ? |
| lim_(x→+∞) (((√(x^3 −3x^2 +7))+((x^4 +3))^(1/3) )/( ((x^6 +2x^5 +1))^(1/4) −((x^7 +2x^3 +3))^(1/5) )) Please show work. |
| A metallic cube is subjected to heating such that as the metal expands, the total surface area increases at rate of 6.25 cm^2 s^(−1) . Calculate the rate at which each side of the cube is increasing when the volume is 51.2 cm^3 . |
| Show that the function y = ∣ x −5 ∣ has no derivative at x = 5. |
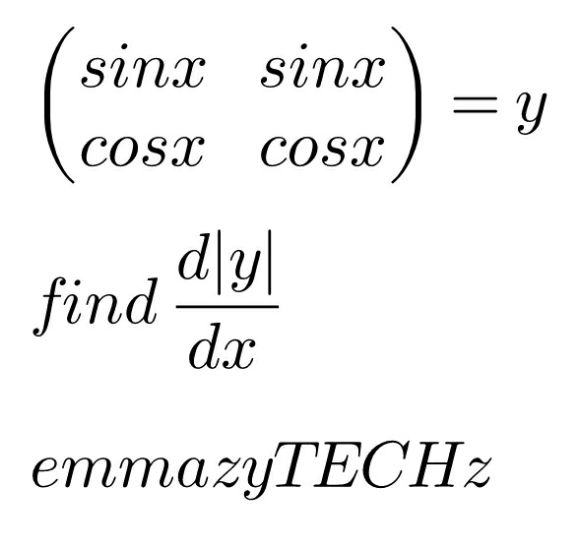
|
| Find the largest possible area of trapezoid that can be drawn under the x−axis so that one of its bases is on the x−axis and the other two vertices are on the curve y=x^2 −9 |
| A man walks along straight path at a speed 4 ft/s. A spotlight is located on the ground 20 ft from the path and is kept focused on the man. At what rate is spotlight rotating when the man is 15 ft from the point on the path closest to the light? |
| For 0≤x≤1 , maximum value of f(x)=x(√(1−x+(√(1−x)))) is __ |