
Question and Answers Forum
DifferentiationQuestion and Answers: Page 9









|
Question and Answers Forum |
DifferentiationQuestion and Answers: Page 9 |
| If the function f is continuous in [a,b] prove that lim_(x→∞ ) ((b−a)/n)Σ_(k=1) ^n f(a+((k(b−a))/n))=∫_a ^b f(x)dx |
| ∫(1/(x+(√(1−x)))) dx |
| solve f(x)= x +(√(x^( 2) −3x +2)) R _f =? R_( f) : rang of f |
|

|

|

|
| (dy/dx)=8x+4y+(2x+y−1)^2 y=? |

|

|
| Find the coordinates of the point on the curve y=3x^2 −2x−5, where the tangent is parallel to the line y−5=8x. |
| ∫_0 ^∞ ((3x^2 )/( (√((5x^2 +1)^3 )))) dx |

|
| solve ∫_2 ^( 3) ⌊ x^( 2) − 2x +5 ⌋dx=? |

|
| 0< x<(π/2) f(x)= ((sin(x) ))^(1/(20)) + ((cos(x)))^(1/(20)) R_( f) =? (Range ) |

|

|

|
| lim_( α→∞) { (α ∫_0 ^( ∞) sin( x^( α) ) dx )=ϕ(α)]= (π/2) −−−− ∫_0 ^( ∞) sin(x^( α) )dx =^(x^( α) = y) (1/α)∫_0 ^( ∞) (( sin(y))/y^( 1−(1/α)) ) dy ⇒ α ∫_0 ^( ∞) sin(x^( α) ) dx = ∫_0 ^( ∞) (( sin(y))/y^( 1−(1/α)) ) dy = (( π)/(2 Γ (1−(1/α))sin ((π/2) (1−(1/α))))) = (π/(2Γ (1−(1/α))cos ((π/(2α)) ))) = ϕ (α ) lim_( α→∞) ϕ (α )=^((1/α) =β) lim_( β→0) (π/(2Γ (1−β)cos ((π/2) β))) = (π/2) |
| Find minimum value of function f(x)=2x−(√(x+1))−(√(x^2 −1)) |
| Ω=∫_0 ^( (π/2)) (( sin^( 2) (x))/((sin(x)+cos(x))^( 6) )) dx=? |
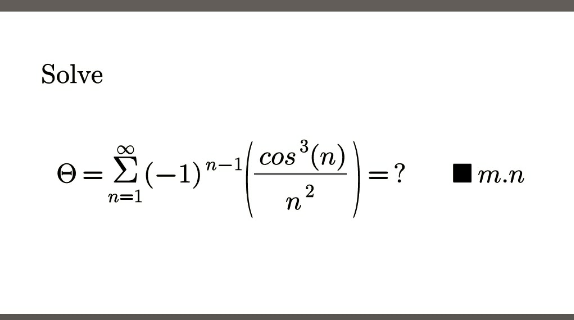
|
| ∫_0 ^( ∞) (( e^( −x) .ln(x).sin(x))/x) dx = −(π/8) (2γ + ln(2)) |
| Calculate If , 𝛗= ∫_0 ^( 1) (( tanh^( −1) ( x^( 3) ))/x) dx = α.ζ( 2) then , α = ? ■ M.N −−−−−−− |
| calculate Ω=∫_0 ^( 1) (( ln(1−x ).ln(1+ x ))/x^( 2) ) dx=? −−−−−−− |