
Question and Answers Forum
Question Number 7191 by Tawakalitu. last updated on 15/Aug/16
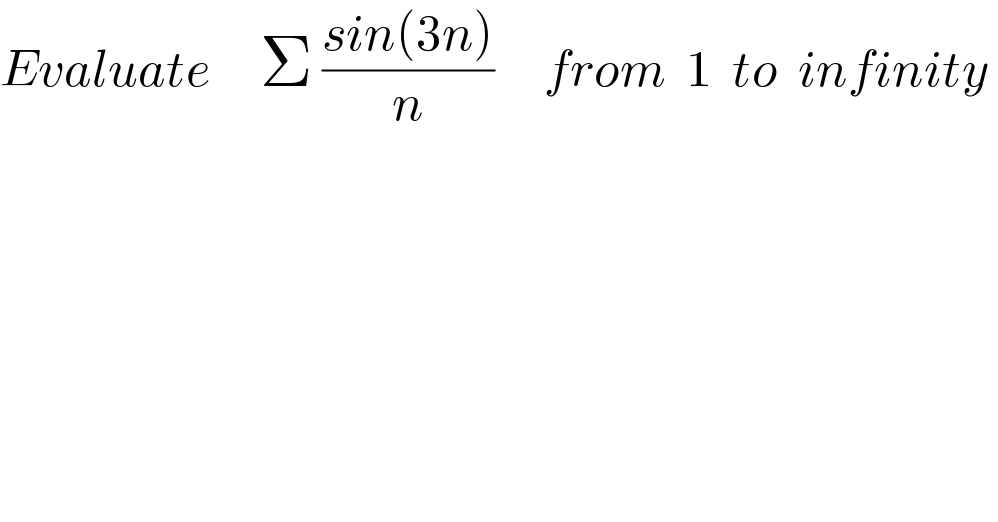
Answered by Yozzia last updated on 15/Aug/16
![Define the function f(x)=x for 0<x<1 , period=2. For Fourier series of f having the form (1) f(x)=(a_0 /2)+Σ_(n=1) ^∞ {a_n cos((nπx)/L)+b_n sin((nπx)/L)}, 2L=2=period⇒L=1, a_0 =(1/L)∫_c ^( c+2L) f(x) dx , c∈R. ∴ For c=0, a_0 =(1/1)∫_0 ^( 2) xdx=(x^2 /2)∣_0 ^2 =2 ⇒(a_0 /2)=1. a_n =(1/L)∫_c ^(c+2L) f(x)cos((nπx)/L)dx n=1,2,3,... Let c=0. ∴ a_n =(1/1)∫_0 ^( 2) xcosnπx dx a_n =(x/(nπ))sinnπx∣_0 ^2 −∫_0 ^2 (1/(nπ))sinnπxdx a_n =(1/(n^2 π^2 ))cosnπx∣_0 ^2 =(1/(n^2 π^2 ))(cos2nπ−1)=0 b_n =(1/L)∫_c ^( c+2L) f(x)sin((nπx)/L)dx (n=1,2,3,...) Take c=0. ∴ b_n =(1/1)∫_0 ^( 2) xsinnπx dx b_n =((−xcosnπx)/(nπ))∣_0 ^2 −∫_0 ^2 ((−cosnπx)/(nπ))dx b_n =((−2)/(nπ))+[(1/(n^2 π^2 ))sinnπx]_0 ^2 b_n =((−2)/(nπ))+0=((−2)/(nπ)) (n≠0). ∴ in (1) x=1+Σ_(n=1) ^∞ ((−2sinnπx)/(nπ)) x=1−(2/π)Σ_(n=1) ^∞ ((sinnπx)/n) Let x=(3/π)∉Z (If x∈Z, x is a point of discontinuity whose output is given by ((f(x+0)+f(x−0))/2)) ∴ (3/π)=1−(2/π)Σ_(n=1) ^∞ ((sin3n)/n) ⇒Σ_(n=1) ^∞ ((sin3n)/n)=(π/2)(1−(3/π)) Σ_(n=1) ^∞ ((sin3n)/n)=((π−3)/2)](Q7194.png)
Commented by Tawakalitu. last updated on 15/Aug/16
| ||
Question and Answers Forum | ||
Question Number 7191 by Tawakalitu. last updated on 15/Aug/16 | ||
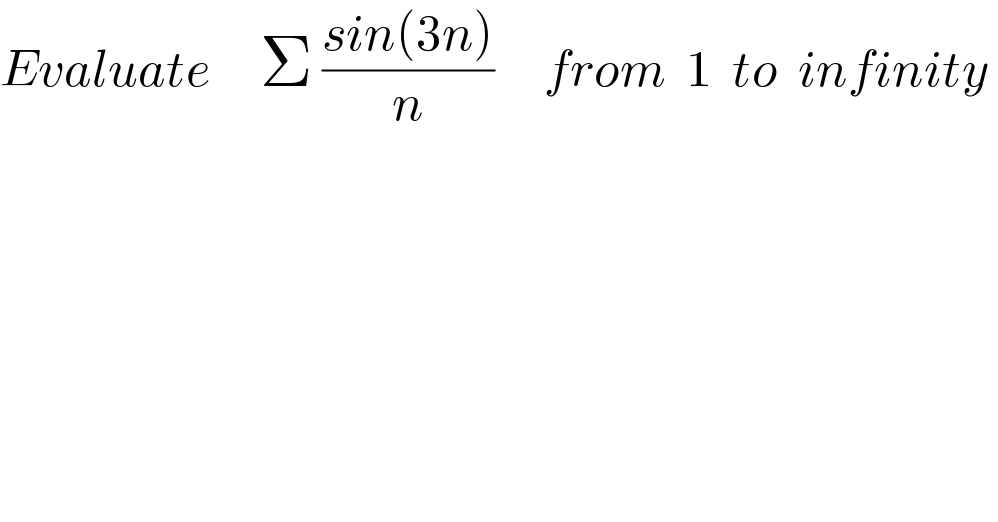 | ||
Answered by Yozzia last updated on 15/Aug/16 | ||
![Define the function f(x)=x for 0<x<1 , period=2. For Fourier series of f having the form (1) f(x)=(a_0 /2)+Σ_(n=1) ^∞ {a_n cos((nπx)/L)+b_n sin((nπx)/L)}, 2L=2=period⇒L=1, a_0 =(1/L)∫_c ^( c+2L) f(x) dx , c∈R. ∴ For c=0, a_0 =(1/1)∫_0 ^( 2) xdx=(x^2 /2)∣_0 ^2 =2 ⇒(a_0 /2)=1. a_n =(1/L)∫_c ^(c+2L) f(x)cos((nπx)/L)dx n=1,2,3,... Let c=0. ∴ a_n =(1/1)∫_0 ^( 2) xcosnπx dx a_n =(x/(nπ))sinnπx∣_0 ^2 −∫_0 ^2 (1/(nπ))sinnπxdx a_n =(1/(n^2 π^2 ))cosnπx∣_0 ^2 =(1/(n^2 π^2 ))(cos2nπ−1)=0 b_n =(1/L)∫_c ^( c+2L) f(x)sin((nπx)/L)dx (n=1,2,3,...) Take c=0. ∴ b_n =(1/1)∫_0 ^( 2) xsinnπx dx b_n =((−xcosnπx)/(nπ))∣_0 ^2 −∫_0 ^2 ((−cosnπx)/(nπ))dx b_n =((−2)/(nπ))+[(1/(n^2 π^2 ))sinnπx]_0 ^2 b_n =((−2)/(nπ))+0=((−2)/(nπ)) (n≠0). ∴ in (1) x=1+Σ_(n=1) ^∞ ((−2sinnπx)/(nπ)) x=1−(2/π)Σ_(n=1) ^∞ ((sinnπx)/n) Let x=(3/π)∉Z (If x∈Z, x is a point of discontinuity whose output is given by ((f(x+0)+f(x−0))/2)) ∴ (3/π)=1−(2/π)Σ_(n=1) ^∞ ((sin3n)/n) ⇒Σ_(n=1) ^∞ ((sin3n)/n)=(π/2)(1−(3/π)) Σ_(n=1) ^∞ ((sin3n)/n)=((π−3)/2)](Q7194.png) | ||
| ||
Commented by Tawakalitu. last updated on 15/Aug/16 | ||
 | ||