
Question and Answers Forum
Question Number 6475 by WAI LIN last updated on 28/Jun/16
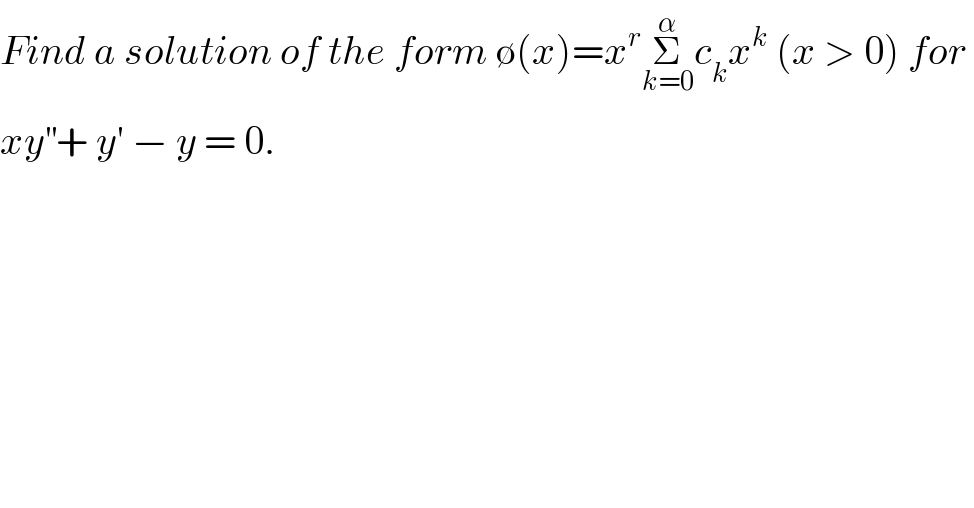
Commented by Yozzii last updated on 29/Jun/16

Commented by nburiburu last updated on 29/Jun/16
![xy′′+y′=(xy′)′=y if y=x^w ⇒ (w)^2 .x^(w−1) =x^w which is impossible for w∈R so the only way to continue would be to assume w=w(x) y=x^(w(x)) ⇒(w.x^w )′=x^w [w′(1+ln x)+w^2 /x]=x^w w′(1+lnx)+(w^2 /x)=1 w′(x+xlnx)+w^2 =x homogeneus solution: w′(x+xlnx)+w^2 =0 (1/w_h ^2 ) dw_h = ((−1)/(x(1+lnx)))dx −(1/w_h ) = − ln(1+lnx) w_h =(1/(ln(1+lnx))) Note: for the eq to have the structure mention as φ(x) the eq should be x^2 y′′+xy′−y=0](Q6496.png)
Commented by WAI LIN last updated on 01/Jul/16
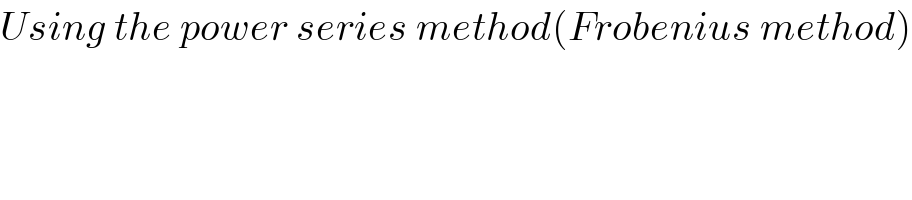
| ||
Question and Answers Forum | ||
Question Number 6475 by WAI LIN last updated on 28/Jun/16 | ||
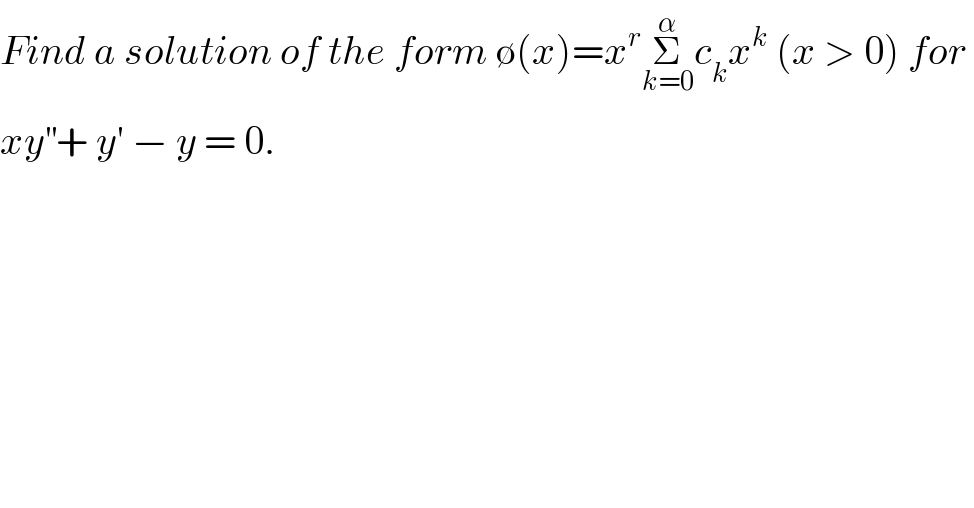 | ||
Commented by Yozzii last updated on 29/Jun/16 | ||
 | ||
Commented by nburiburu last updated on 29/Jun/16 | ||
![xy′′+y′=(xy′)′=y if y=x^w ⇒ (w)^2 .x^(w−1) =x^w which is impossible for w∈R so the only way to continue would be to assume w=w(x) y=x^(w(x)) ⇒(w.x^w )′=x^w [w′(1+ln x)+w^2 /x]=x^w w′(1+lnx)+(w^2 /x)=1 w′(x+xlnx)+w^2 =x homogeneus solution: w′(x+xlnx)+w^2 =0 (1/w_h ^2 ) dw_h = ((−1)/(x(1+lnx)))dx −(1/w_h ) = − ln(1+lnx) w_h =(1/(ln(1+lnx))) Note: for the eq to have the structure mention as φ(x) the eq should be x^2 y′′+xy′−y=0](Q6496.png) | ||
Commented by WAI LIN last updated on 01/Jul/16 | ||
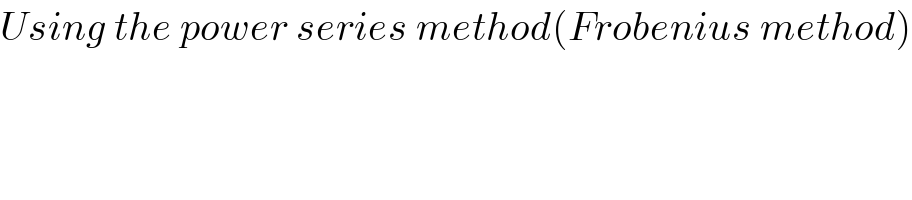 | ||