
Question and Answers Forum
Question Number 119849 by benjo_mathlover last updated on 27/Oct/20
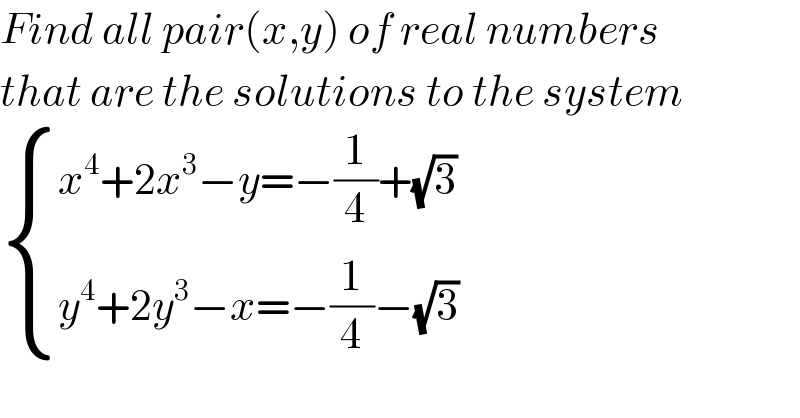
Answered by 1549442205PVT last updated on 27/Oct/20

| ||
Question and Answers Forum | ||
Question Number 119849 by benjo_mathlover last updated on 27/Oct/20 | ||
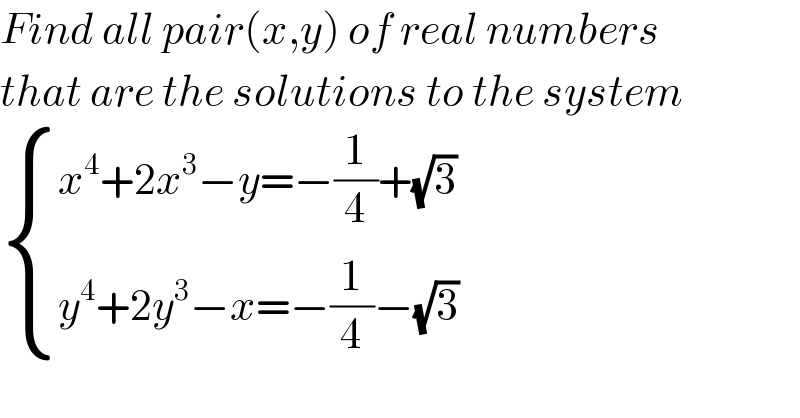 | ||
Answered by 1549442205PVT last updated on 27/Oct/20 | ||
 | ||
| ||