
Question and Answers Forum
Question Number 151097 by naka3546 last updated on 18/Aug/21
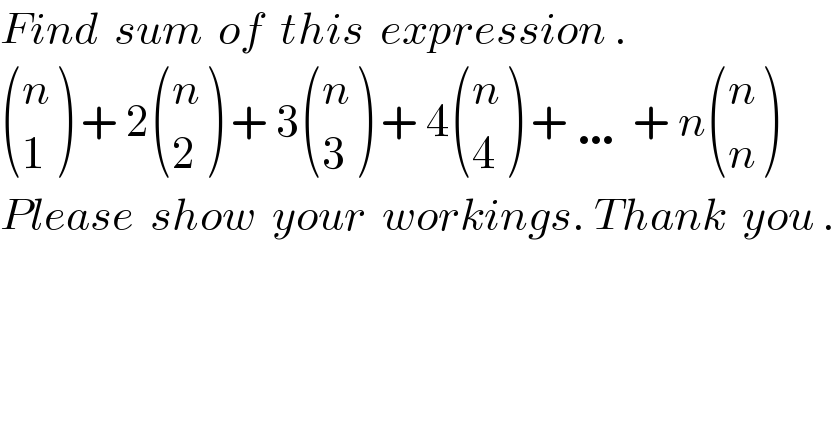
Answered by Olaf_Thorendsen last updated on 18/Aug/21
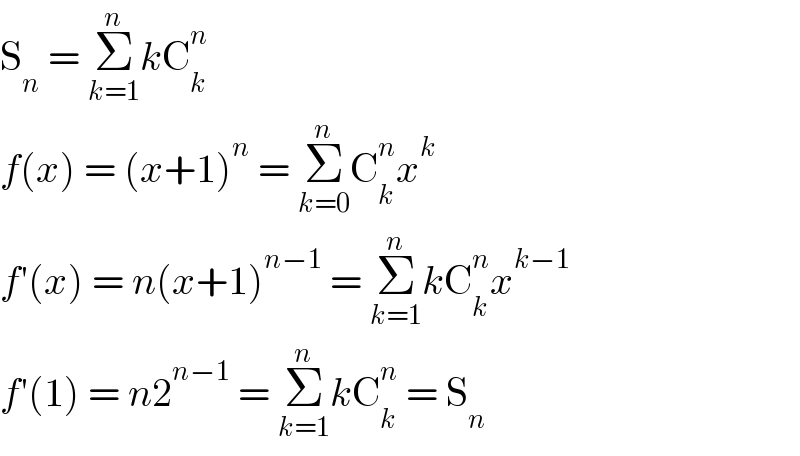
Answered by mr W last updated on 18/Aug/21
![S_n = ((n),(1) ) + 2 ((n),(2) ) + 3 ((n),(3) ) + 4 ((n),(4) ) + … + n ((n),(n) ) S_n =0 ((n),(0) )+ ((n),(1) ) + 2 ((n),(2) ) + 3 ((n),(3) ) + 4 ((n),(4) ) + … + n ((n),(n) ) S_n =n ((n),(n) )+(n−1) ((n),((n−1)) ) +(n− 2) ((n),((n−2)) ) +(n− 3) ((n),((n−3)) ) + … + 0 ((n),((n−n)) ) S_n =n ((n),(0) )+(n−1) ((n),(1) ) +(n− 2) ((n),(2) ) +(n− 3) ((n),(3) ) + … + 0 ((n),(n) ) 2S_n =n[ ((n),(0) )+ ((n),(1) ) + ((n),(2) ) + ((n),(3) ) + … + ((n),(n) )] 2S_n =n×2^n ⇒S_n =n×2^(n−1)](Q151129.png)
| ||
Question and Answers Forum | ||
Question Number 151097 by naka3546 last updated on 18/Aug/21 | ||
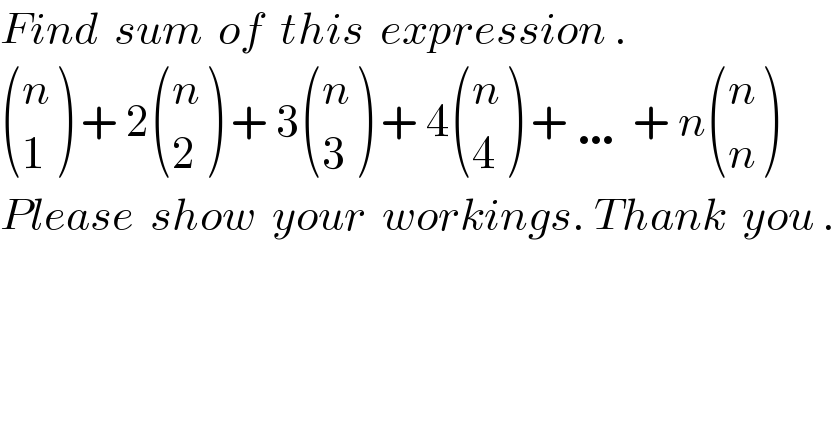 | ||
Answered by Olaf_Thorendsen last updated on 18/Aug/21 | ||
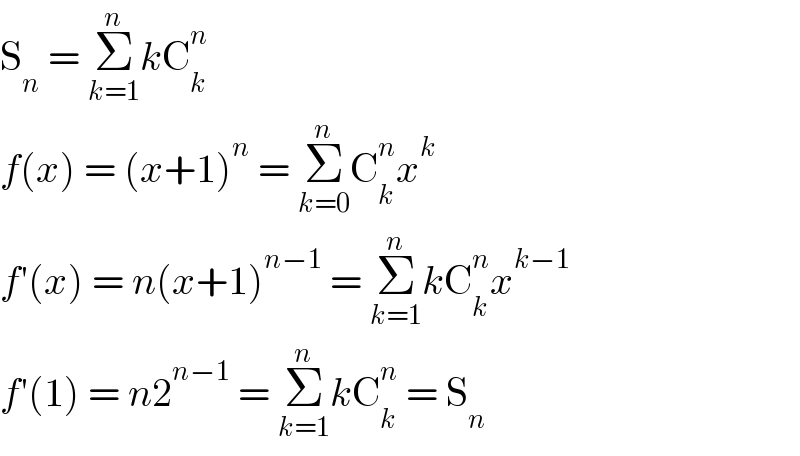 | ||
| ||
Answered by mr W last updated on 18/Aug/21 | ||
![S_n = ((n),(1) ) + 2 ((n),(2) ) + 3 ((n),(3) ) + 4 ((n),(4) ) + … + n ((n),(n) ) S_n =0 ((n),(0) )+ ((n),(1) ) + 2 ((n),(2) ) + 3 ((n),(3) ) + 4 ((n),(4) ) + … + n ((n),(n) ) S_n =n ((n),(n) )+(n−1) ((n),((n−1)) ) +(n− 2) ((n),((n−2)) ) +(n− 3) ((n),((n−3)) ) + … + 0 ((n),((n−n)) ) S_n =n ((n),(0) )+(n−1) ((n),(1) ) +(n− 2) ((n),(2) ) +(n− 3) ((n),(3) ) + … + 0 ((n),(n) ) 2S_n =n[ ((n),(0) )+ ((n),(1) ) + ((n),(2) ) + ((n),(3) ) + … + ((n),(n) )] 2S_n =n×2^n ⇒S_n =n×2^(n−1)](Q151129.png) | ||
| ||