Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 68145 by Joel122 last updated on 06/Sep/19

$$\mathrm{Find}\mathrm{the}\mathrm{arc}\mathrm{length},\mathrm{given}\mathrm{the}\mathrm{curve}$$$$x\left(t\right)=\sin \left(\pi t\right),y\left(t\right)=t,0⩽t⩽1$$

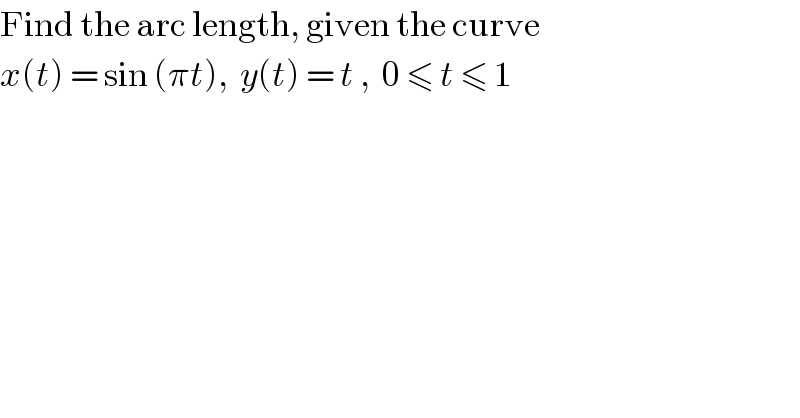
Commented by Joel122 last updated on 06/Sep/19

$$x^{\prime }\left(t\right)=\pi \cos \left(\pi t\right),y^{\prime }\left(t\right)=1$$$$$$$$L={\int }_0^1\sqrt{{\left(x^{\prime }\left(t\right)\right)}^2+{\left(y^{\prime }\left(t\right)\right)}^2}dt$$$$={\int }_0^1\sqrt{{\pi }^2{\cos }^2\left(\pi t\right)+1}dt$$$$$$$${\mathrm{I}}^{\prime }\mathrm{m}\mathrm{stuck}\mathrm{with}\mathrm{the}\mathrm{integral}.\mathrm{Please}\mathrm{help}$$

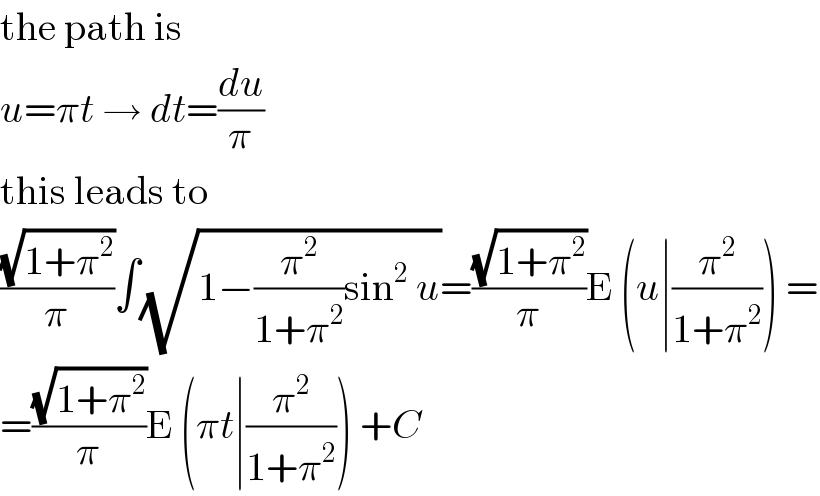
Commented by MJS last updated on 06/Sep/19

$$\mathrm{this}{\mathrm{can}}^{\prime }\mathrm{t}\mathrm{be}\mathrm{solved}\mathrm{using}\mathrm{elementary}\mathrm{calculus}$$$${\mathrm{it}}^{\prime }\mathrm{s}\mathrm{an}ellipticintegral$$

Commented by MJS last updated on 06/Sep/19

https://en.m.wikipedia.org/wiki/Elliptic_integral

Commented by Joel122 last updated on 06/Sep/19

$$thankyouSir$$

Commented by MJS last updated on 06/Sep/19

$$\mathrm{the}\mathrm{path}\mathrm{is}$$$$u=\pi t\to dt=\frac{du}{\pi }$$$$\mathrm{this}\mathrm{leads}\mathrm{to}$$$$\frac{\sqrt{1+{\pi }^2}}{\pi }\int \sqrt{1-\frac{{\pi }^2}{1+{\pi }^2}{\sin }^{2}u}=\frac{\sqrt{1+{\pi }^2}}{\pi }\mathrm{E}(u\mid \frac{{\pi }^2}{1+{\pi }^2})=$$$$=\frac{\sqrt{1+{\pi }^2}}{\pi }\mathrm{E}(\pi t\mid \frac{{\pi }^2}{1+{\pi }^2})+C$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com