
Question and Answers Forum
Question Number 137597 by bemath last updated on 04/Apr/21

Answered by EDWIN88 last updated on 04/Apr/21

Answered by mr W last updated on 04/Apr/21
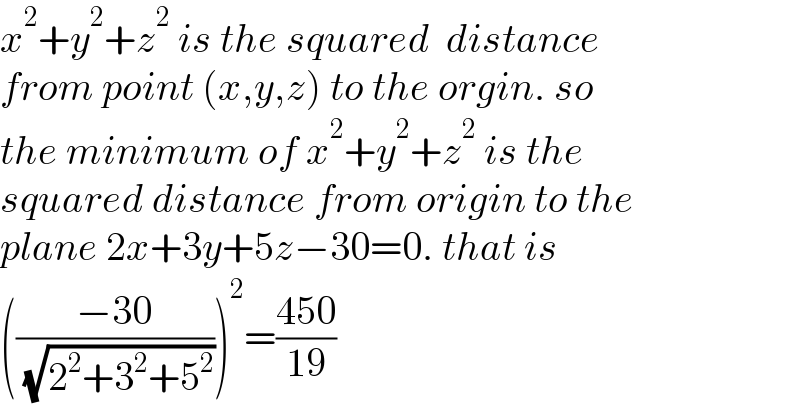
Commented by otchereabdullai@gmail.com last updated on 04/Apr/21

| ||
Question and Answers Forum | ||
Question Number 137597 by bemath last updated on 04/Apr/21 | ||
 | ||
Answered by EDWIN88 last updated on 04/Apr/21 | ||
 | ||
Answered by mr W last updated on 04/Apr/21 | ||
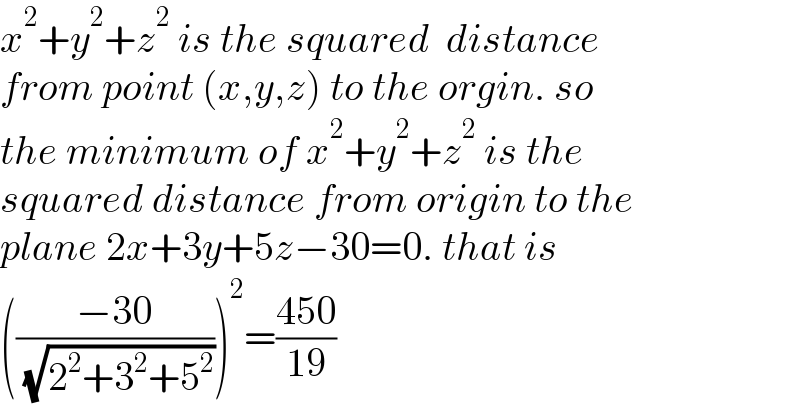 | ||
| ||
Commented by otchereabdullai@gmail.com last updated on 04/Apr/21 | ||
 | ||