
Question and Answers Forum
Question Number 21825 by Joel577 last updated on 05/Oct/17
![Find the simplest form of Σ_(k = 1) ^n 2^k [sin^2 (((2kπ)/3)) + (1/4)]](Q21825.png)
Commented by sma3l2996 last updated on 05/Oct/17

Commented by Joel577 last updated on 05/Oct/17
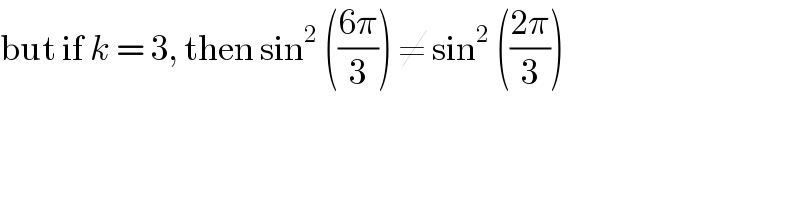
| ||
Question and Answers Forum | ||
Question Number 21825 by Joel577 last updated on 05/Oct/17 | ||
![Find the simplest form of Σ_(k = 1) ^n 2^k [sin^2 (((2kπ)/3)) + (1/4)]](Q21825.png) | ||
Commented by sma3l2996 last updated on 05/Oct/17 | ||
 | ||
Commented by Joel577 last updated on 05/Oct/17 | ||
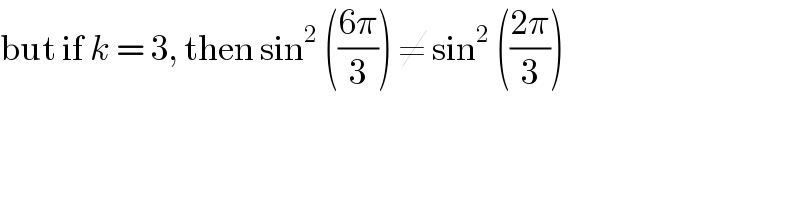 | ||