
Question and Answers Forum
Question Number 184819 by cortano1 last updated on 12/Jan/23
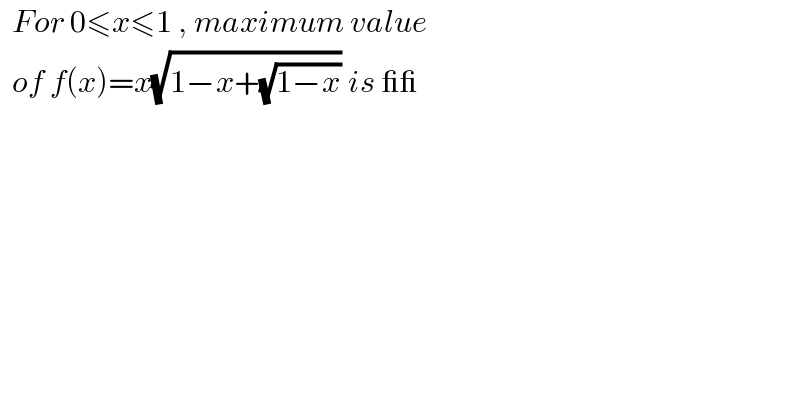
Answered by Frix last updated on 12/Jan/23
![f′(x)=0 −((5x−4+2(3x−2)(√(1−x)))/(4(√(1−x))(√(1−x+(√(1−x))))))=0 2(3x−2)(√(1−x))=4−5x Squaring and transforming x(x^2 −((59)/(36))x+(2/3))=0 x=0 [obviously wrong as f′(0)=(√2)] x=(8/9) [also wrong as f′((8/9))=−1] x=(3/4) [f′((3/4))=0] f((3/4))=((3(√3))/8)](Q184850.png)
Answered by Frix last updated on 12/Jan/23
![Let t=(√(1−x))≥0 ⇔ x=1−t^2 f(t)=(1−t^2 )(√(t^2 +t)) f′(t)=0 −((6t^3 +5t^2 −2t−1)/(2(√(t^2 +t))))=0 t=−1 [wrong] t=−(1/3) [wrong] t=(1/2) ⇒ x=(3/4)](Q184851.png)
| ||
Question and Answers Forum | ||
Question Number 184819 by cortano1 last updated on 12/Jan/23 | ||
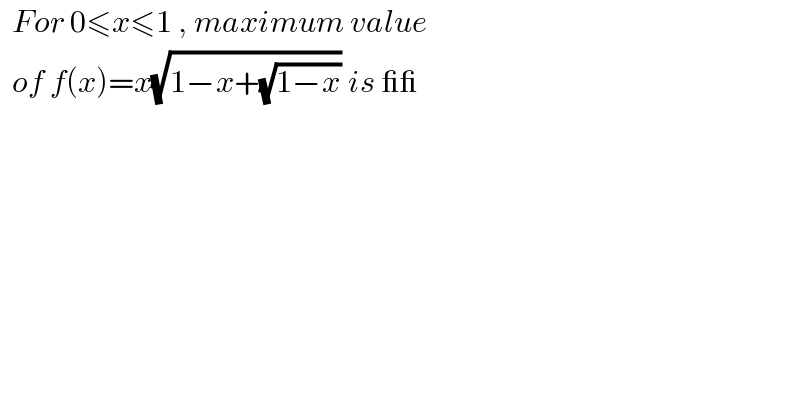 | ||
Answered by Frix last updated on 12/Jan/23 | ||
![f′(x)=0 −((5x−4+2(3x−2)(√(1−x)))/(4(√(1−x))(√(1−x+(√(1−x))))))=0 2(3x−2)(√(1−x))=4−5x Squaring and transforming x(x^2 −((59)/(36))x+(2/3))=0 x=0 [obviously wrong as f′(0)=(√2)] x=(8/9) [also wrong as f′((8/9))=−1] x=(3/4) [f′((3/4))=0] f((3/4))=((3(√3))/8)](Q184850.png) | ||
| ||
Answered by Frix last updated on 12/Jan/23 | ||
![Let t=(√(1−x))≥0 ⇔ x=1−t^2 f(t)=(1−t^2 )(√(t^2 +t)) f′(t)=0 −((6t^3 +5t^2 −2t−1)/(2(√(t^2 +t))))=0 t=−1 [wrong] t=−(1/3) [wrong] t=(1/2) ⇒ x=(3/4)](Q184851.png) | ||
| ||