
Question and Answers Forum
GeometryQuestion and Answers: Page 101








Pg 96 Pg 97 Pg 98 Pg 99 Pg 100 Pg 101 Pg 102 Pg 103 Pg 104 Pg 105
|
Question and Answers Forum |
GeometryQuestion and Answers: Page 101 |
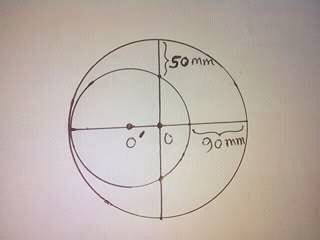
| A semicircle is tangent to both legs of a right triangle and has its centre on the hypotenuse. The hypotenuse is partitioned into 4 segments, with lengths 3, 12, 12, and x, as shown in the figure. Determine the value of ′x′. |
| Let ABC be an acute-angled triangle with AC ≠ BC and let O be the circumcenter and F be the foot of altitude through C. Further, let X and Y be the feet of perpendiculars dropped from A and B respectively to (the extension of) CO. The line FO intersects the circumcircle of ΔFXY, second time at P. Prove that OP < OF. |

|

|
| ∫sin x |
| Let PQRS be a rectangle such that PQ = a and QR = b. Suppose r_1 is the radius of the circle passing through P and Q and touching RS and r_2 is the radius of the circle passing through Q and R and touching PS. Show that : 5(a + b) ≤ 8(r_1 + r_2 ) |
| y = ∣sin x∣ + 2 y = ∣x∣ + 2 −π −π ≤ x ≤ π Find the area that have created from the equations above |
| Find the side lengths of a triangle if side lengths are consecutive integers,and one of whose angles is twice as large as another. |
| x−5×+3=7 |
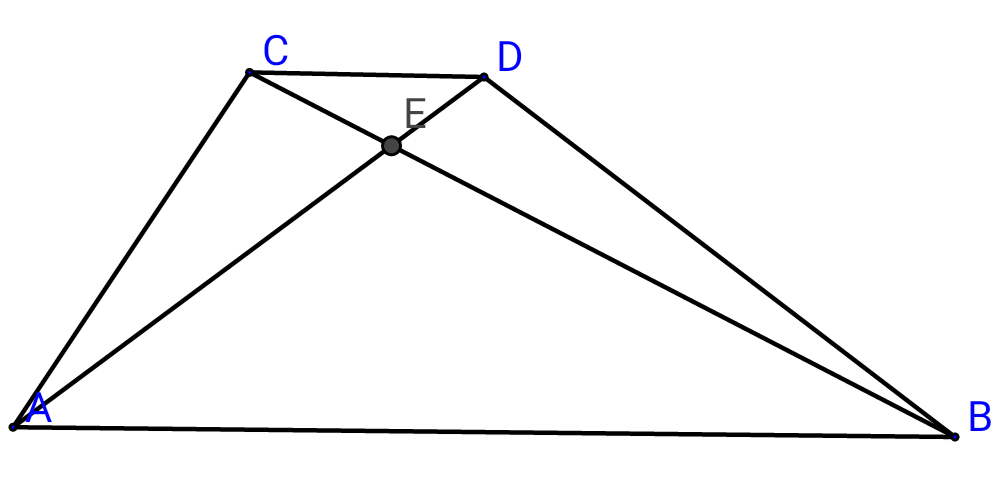
| Let ABCD be a parallelogram. Two points E and F are chosen on the sides BC and CD, respectively, such that ((EB)/(EC)) = m, and ((FC)/(FD)) = n. Lines AE and BF intersect at G. Prove that the ratio ((AG)/(GE)) = (((m + 1)(n + 1))/(mn)). |
| from 1 to 100 isn′t(10,20,30,40,50,60,70,80,90,100), totalizing 10 times the number 0 apears from 1 to 100? |
| F[topology]={G⊂X.G is finit.} please sol it |

|

|
| Σ((cos 2rθ)/(sin^2 2rθ−sin^2 θ)) |
| ∫ (dx/(1 − sin x + cos x)) |
| Imtegrate ∫e^(−ax^2 +bx+c) dx for a>0. It′s just for fun. If you have questions leave a comment. I′ll do my best to answer them. |
| ∫secxdx |

|

|

|

|
| Ball A is dropped from the top of a building. At the same instant ball B is thrown vertically upwards from the ground. When the ball collide, they are moving in opposite directions and the speed of A(u) is twice the speed of B. The relative velocity of the ball just before collision and relative acceleration between them is (only their magnitudes) (A) 0 and 0 (B) ((3u)/2) and 0 (C) ((3u)/2) and 2g (D) ((3u)/2) and g |

|

|

|
Pg 96 Pg 97 Pg 98 Pg 99 Pg 100 Pg 101 Pg 102 Pg 103 Pg 104 Pg 105 |