
Question and Answers Forum
GeometryQuestion and Answers: Page 102



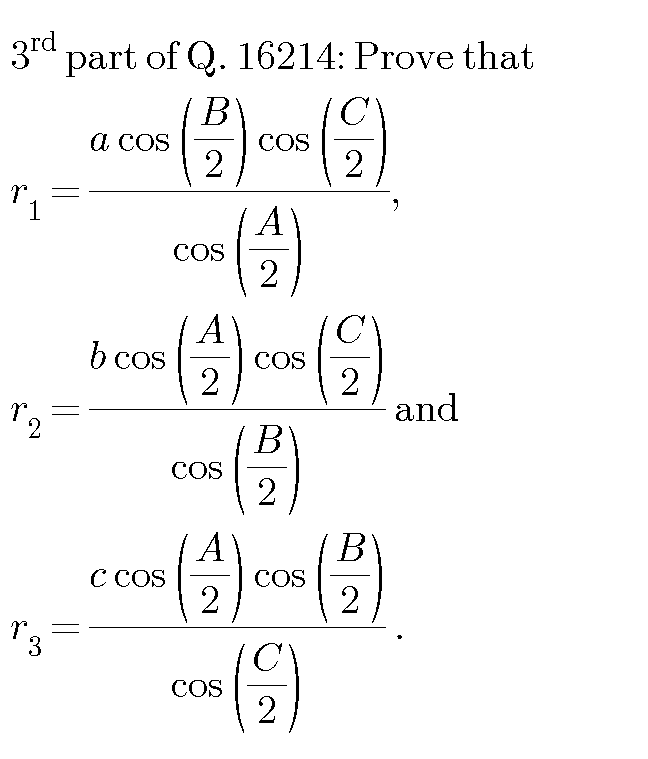



Pg 97 Pg 98 Pg 99 Pg 100 Pg 101 Pg 102 Pg 103 Pg 104 Pg 105 Pg 106
|
Question and Answers Forum |
GeometryQuestion and Answers: Page 102 |
| The maximum value of cos^2 (cos (33π + θ)) + sin^2 (sin (45π + θ)) is (1) 1 + sin^2 1 (2) 2 (3) 1 + cos^2 1 (4) cos^2 2 |
| Let M be a point in the interior of the equilateral triangle ABC and let A′, B′ and C′ be its projections onto the sides BC, CA and AB, respectively. Prove that the sum of lengths of the inradii of triangles MAC′, MBA′ and MCB′ equals the sum of lengths of the inradii of trianges MAB′, MBC′ and MCA′. |
| Prove that the segments joining the midpoints of the opposite sides of an equiangular hexagon are concurrent. |
| A convex hexagon is given in which any two opposite sides have the following property: the distance between their midpoints is ((√3)/2) times the sum of their lengths. Prove that the hexagon is equiangular. |
| The side lengths of an equiangular octagon are rational numbers. Prove that the octagon has a symmetry center. |
| Let a_1 , a_2 , ..., a_n be the side lengths of an equiangular polygon. Prove that if a_1 ≥ a_2 ≥ ... ≥ a_n , then the polygon is regular. |
| An equiangular polygon with an odd number of sides is inscribed in a circle. Prove that the polygon is regular. |

|

|
| Prove that p is a prime number if and only if every equiangular polygon with p sides of rational lengths is regular. |

|
| please what does the question mean by the overlapping portion of A and B. |

|
| A,B and E are three circles all with radius 1 unit.A and E touch at P whole B and E touch at Q. ∠POQ=x° where O is the centre of E.Find the area of the overlapping portion of A and B if 0≤x≤60° |

|

|

|
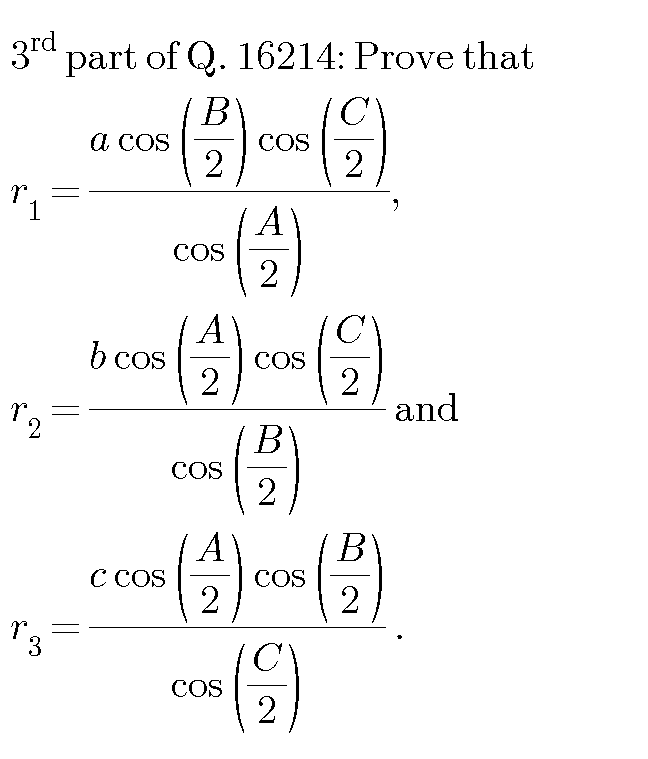
|

|
| Related to Q16140 What if the three lines d_1 ,d_2 ,d_3 are not parallel, but concurrent? |

|

|
| In ΔABC, r_1 , r_2 and r_3 are the exradii as shown. Prove that r_1 = (Δ/(s − a)) , r_2 = (Δ/(s − b)) and r_3 = (Δ/(s − c)) . Here s = ((a + b + c)/2) . |

|

|
| let a_1 >a_2 >0 and a_(n+1) =(√(a_n a_(n−1 ) )) where n is greater than equal to 2 Then The sequence {a_(2n) } is (1) monotonic increasing (2)monotonic decreasing (3)non monotonic (4)unbounded |
Pg 97 Pg 98 Pg 99 Pg 100 Pg 101 Pg 102 Pg 103 Pg 104 Pg 105 Pg 106 |