
Question and Answers Forum
GeometryQuestion and Answers: Page 103








Pg 98 Pg 99 Pg 100 Pg 101 Pg 102 Pg 103 Pg 104 Pg 105 Pg 106 Pg 107
|
Question and Answers Forum |
GeometryQuestion and Answers: Page 103 |

|

|
| Σ((cos 2rθ)/(sin^2 2rθ−sin^2 θ)) |
| ∫ (dx/(1 − sin x + cos x)) |
| Imtegrate ∫e^(−ax^2 +bx+c) dx for a>0. It′s just for fun. If you have questions leave a comment. I′ll do my best to answer them. |
| ∫secxdx |

|

|

|

|
| Ball A is dropped from the top of a building. At the same instant ball B is thrown vertically upwards from the ground. When the ball collide, they are moving in opposite directions and the speed of A(u) is twice the speed of B. The relative velocity of the ball just before collision and relative acceleration between them is (only their magnitudes) (A) 0 and 0 (B) ((3u)/2) and 0 (C) ((3u)/2) and 2g (D) ((3u)/2) and g |

|

|

|
| A line segment moves in the plane with its end points on the coordinate axes so that the sum of the length of its intersect on the coordinate axes is a constant C . Find the locus of the mid points of this segment . Ans. is 8(∣x∣^3 +∣y∣^3 )=C . Λ means power . pls. solve it. |
| The triangle ABC has CA = CB. P is a point on the circumcircle between A and B (and on the opposite side of the line AB to C). D is the foot of the perpendicular from C to PB. Show that PA + PB = 2∙PD. |

|
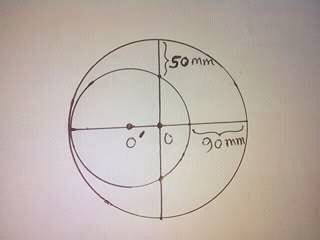
| The circle ω touches the circle Ω internally at P. The centre O of Ω is outside ω. Let XY be a diameter of Ω which is also tangent to ω. Assume PY > PX. Let PY intersect ω at Z. If YZ = 2PZ, what is the magnitude of ∠PYX in degrees? |
| Find the coordinate of the point in RΛ3 which is the reflection the point (1,2,3) with respect to plane X+Y+Z=1 . |
| Between 2:00 and 2:15, what time is it exactly when the hour, minute, and second′s hand of a clock occupy the same angular position. |
| 3x−4y=0,4y−5z=0,5z−3x=0 then x,y,z is AP,GP,HP,AGP?????? |
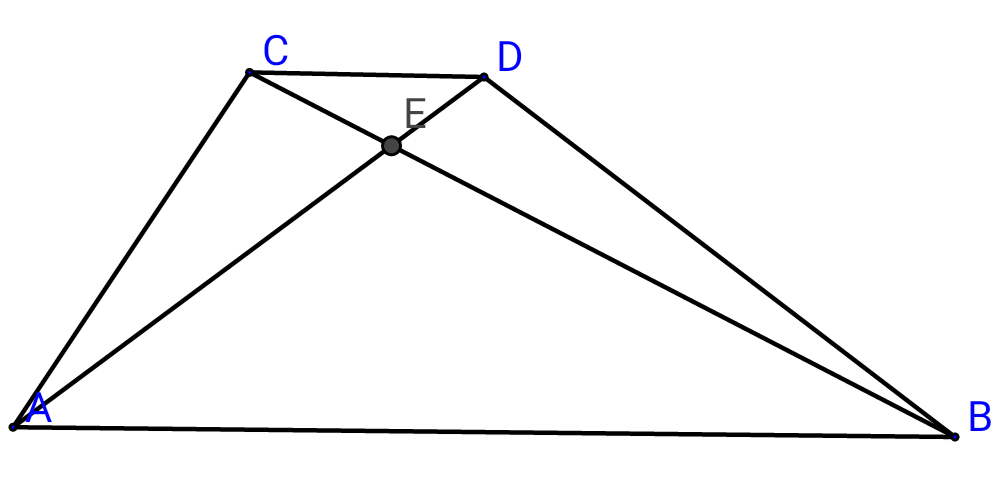
| Suppose that the point M lying in the interior of the parallelogram ABCD, two parallels to AB and AD are drawn, intersecting the sides of ABCD at the points P, Q, R, S (See Figure). Prove that M lies on the diagonal AC if and only if [MRDS] = [MPBQ]. |
| Find the point in interior of a convex quadrilateral such that the sum of its distances to the 4 vertices is minimal. Find the point in interior of a convex quadrilateral such that the sum of its distances to the 4 sides is minimal. |
| The intersection of the ABC triangle median is at G point. The corner of the BGC is 90°. If the AG cut length is 12 cm, locate the BC side. |

|
| Please solve Q. 16069. Ask from me the solution if needed and please explain it. |
Pg 98 Pg 99 Pg 100 Pg 101 Pg 102 Pg 103 Pg 104 Pg 105 Pg 106 Pg 107 |