
Question and Answers Forum
GeometryQuestion and Answers: Page 114



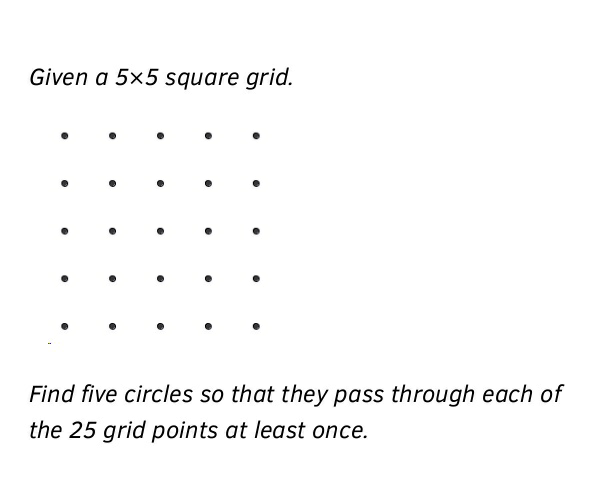




Pg 109 Pg 110 Pg 111 Pg 112 Pg 113 Pg 114 Pg 115 Pg 116 Pg 117 Pg 118
|
Question and Answers Forum |
GeometryQuestion and Answers: Page 114 |

|
| (√(6+(√(6+(√(6+(√(6+(√6))))))))) SOLUTION let x = (√(6+(√(6+(√(6+(√(6+(√6))))))))) therefore.. x^(2 ) = 6+(√(6+(√(6+(√(6+(√(6 )))))))) the equation is a continuos funtion Thus x^2 = 6+(√(6+(√(6+(√(6+(√(6+(√6) ))))))))...... since x = (√(6+(√(6+(√(6+(√(6+(√6))))))))) Therdfore x^2 = 6 + x x^2 − x − 6 = 0 x^2 − 3x + 2x − 6 = 0 (x^2 − 3x) + (2x − 6) = 0 x(x − 3) + 2(x − 3) = 0 (x − 3)(x + 2) = 0 x − 3 = 0 or x − 2 = 0 x = 3 or x = −2 since negative is not allowed Thus x = 6 Meaning that (√(6+(√(6+(√(6+(√(6+(√(6 )))))))))) = 3 DONE THANK YOU SO MUCH. I UNDERSTAND THE SOLUTION. |
| cos α+β ≈(((cos α+cos β)/(cos^(−1) α+cos^(−1) β)))^(α+β) sin a+b≈(((sin a+sin b)/(sin^(−1) a+sin^(−1) b)))^(a+b) tan (a+(a/b))^k ≈(((tan (a+b)×k)/(tan^(−1) (a+b)×k))) |
| ∫_0 ^(π/2) (dx/(sinx^(cosx ) + cosx^(sinx ) )) |

|

|
| ∫4x^2 − (5/(2x^(−2) )) + 4 dx, x≠0 |
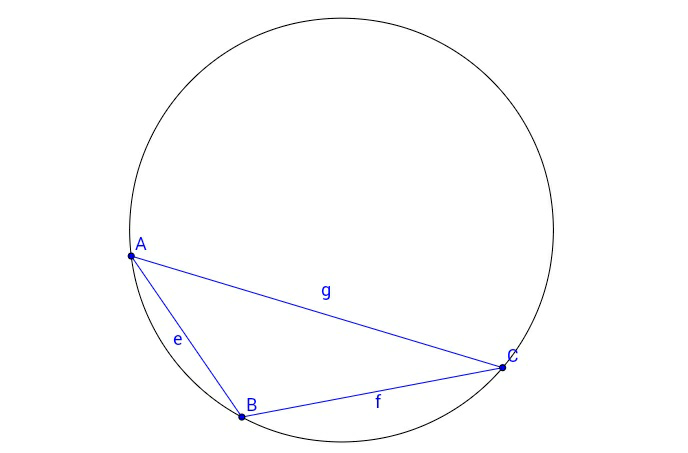
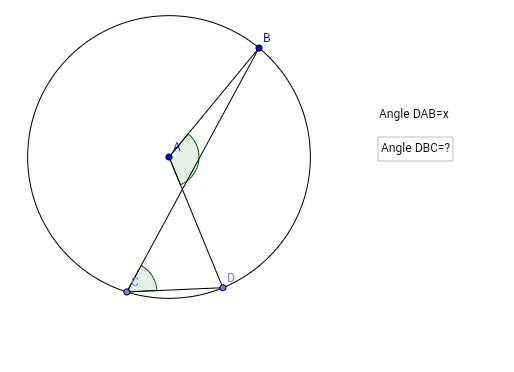
| In a right triangle, the mid-point of the hypotenuse is equidistant from all the three vertices of the triangle. |
| The segment between the mid-points of two sides of a triangle is parallel to the third side and half as long. |
| Triangle ABC has midpoints D, E and F. By connecting each verticie with the opposite midpoint, we create a cress−section called G. Prove that all three lines cross at point G regardless of the type of triangle |
| This is a simple question but for some silly reason I can′t figure it out... 1. If I have a circle with radius r and area A, and I wish to make a new circle with n times the area, for what new value of r should be used? 2. What if I increase the area from A to A+n? What value of r would be used here? |

|
| An ellipse having semi-major axis length a and semi-minor axis length b and a circle having radius r have equal area. Express r in terms of a and b. |
| Divide a circle into two congruent regions such that they have no straightedge. |
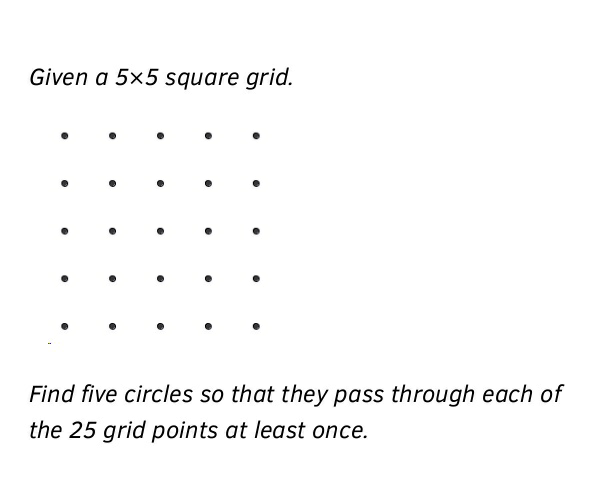
|

|
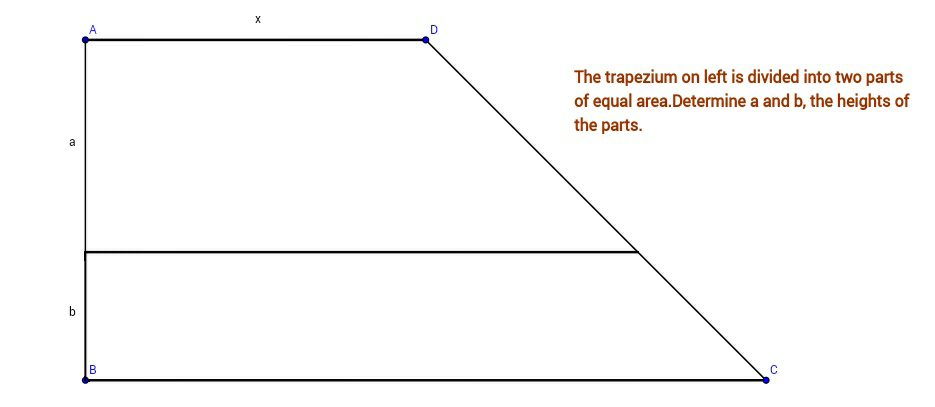
| A circle of radius r_1 has been divided into two parts of equal area, by an arc having center on the circle. Determine the radius(r_2 ) of the arc. |

|

|

|
| hola |

|
| 1+2= |

|
| ^• A kite is a quadrilateral having two pairs of adjacent sides equal. Draw a semi-circle inside it touching all the sides using Eucledian tools. ^• Can we show that the above semi-circle is of the laregest possible area inside the kite? |
| Prove that inside a square, a semi-circle, which touches all the four sides of the square, is possible with ruler and compass. |
Pg 109 Pg 110 Pg 111 Pg 112 Pg 113 Pg 114 Pg 115 Pg 116 Pg 117 Pg 118 |