
Question and Answers Forum
GeometryQuestion and Answers: Page 95
















|
Question and Answers Forum |
GeometryQuestion and Answers: Page 95 |

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
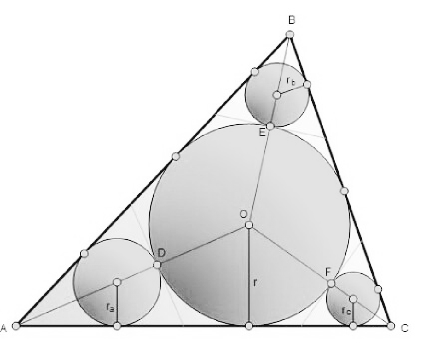
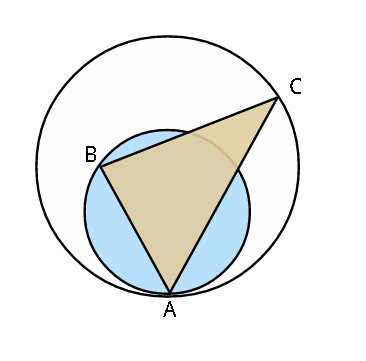
| new idea (and solution) to questions 35178 & 35195 triangle: ABC; a=BC, b=CA, c=AB; α=∠CAB, β=∠ABC, γ=∠BCA d=(√((a+b+c)(a+b−c)(a−b+c)(−a+b+c))) put it as this: A= ((0),(0) ), B= ((c),(0) ), C= ((((−a^2 +b^2 +c^2 )/(2c))),((d/(2c))) ) circumcircle: center=M_1 = (((c/2)),((((a^2 +b^2 −c^2 )c)/(2d))) ) radius=R=((abc)/d) (calculated by intersection of circles with centers A, B, C or of symmetry−axes of AB and AC) 2 circles touching b, c and circumcircle, one from inside, the other from outside: center=M_2 lies on y=kx with k=tan (α/2) M_2 = ((x),((xtan (α/2))) ) radius=r_1 =R−∣M_1 M_2 ∣=xtan (α/2) (inside) r_2 =∣M_1 M_2 ∣−R=xtan (α/2) (outside) (obviously any circle with center M_2 (x) and touching the x−axis has radius xtan (α/2) and also obviously the touching point of 2 circles is located on the line connecting their centers) 1. ∣M_1 M_2 ∣=R−xtan (α/2) M_1 M_2 =(R−xtan (α/2))^2 2. ∣M_1 M_2 ∣=R+xtan (α/2) M_1 M_2 =(R+xtan (α/2))^2 tan (α/2)=((sin (α/2))/(cos (α/2)))=((√((1−cos α)/2))/(√((1+cos α)/2)))=(√((1−cos α)/(1+cos α)))= [cos α=((−a^2 +b^2 +c^2 )/(2bc))] =(√((a^2 −b^2 +2bc−c^2 )/(−a^2 +b^2 +2bc+c^2 )))=(√(((a+b−c)(a−b+c))/((a+b+c)(−a+b+c)))) M_1 M_2 =(m_1 −m_2 )^2 +(n_1 −n_2 )^2 = =((c/2)−x)^2 +((((a^2 +b^2 −c^2 )c)/(2d))−xtan (α/2))^2 = [after some transformation work] =((4bc)/((a+b+c)(−a+b+c)))x^2 −((2bc(b+c))/((a+b+c)(−a+b+c)))x+((a^2 b^2 c^2 )/d^2 ) [((a^2 b^2 c^2 )/d^2 )=R^2 ] (R±xtan (α/2))^2 =x^2 tan^2 (α/2)±2Rxtan (α/2)+R^2 = =(((a+b−c)(a−b+c))/((a+b+c)(−a+b+c)))x^2 ±((2abc)/((a+b+c)(−a+b+c)))x+R^2 so we have ((4bc)/((a+b+c)(−a+b+c)))x^2 −((2bc(b+c))/((a+b+c)(−a+b+c)))x= =(((a+b−c)(a−b+c))/((a+b+c)(−a+b+c)))x^2 ±((2abc)/((a+b+c)(−a+b+c)))x which leads to x_3 =0 (as I explained before, the point A can be seen as a circle with radius 0 still meeting the requirements) x_1 =((2bc)/(a+b+c)) ⇒ r_1 =2bc(√(((a+b−c)(a−b+c))/((a+b+c)^3 (−a+b+c)))) x_2 =((2bc)/(−a+b+c)) ⇒ r_2 =2bc(√(((a+b−c)(a−b+c))/((a+b+c)(−a+b+c)^3 ))) for the circles corresponding with the points B and C just interchange {a, b, c} with {b, c, a} and {c, a, b} |

|

|

|

|

|

|

|

|