Given a,b and c are real numbers and a<b<c. If (1/a) + (1/b) + (1/c) = (1/(18)) , find minimum value of a.


Question and Answers Forum

All Questions Topic List
Number Theory Questions
Previous in All Question Next in All Question
Previous in Number Theory Next in Number Theory
Question Number 134069 by john_santu last updated on 27/Feb/21

$G i v e n a, b a n d c a r e r e a l n u m b e r s a n d a < b < c .$ $I f \frac{1}{a} + \frac{1}{b} + \frac{1}{c} = \frac{1}{18}, f i n d m i n i m u m v a l u e o f a .$
Commented by mr W last updated on 27/Feb/21

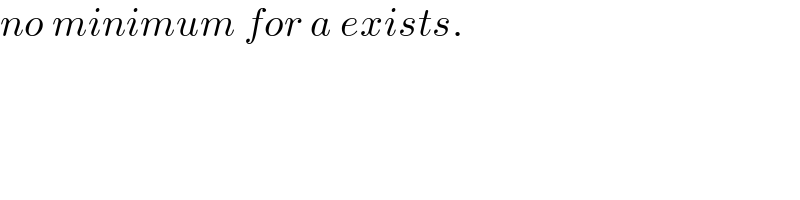
$n o m i n i m u m f o r a e x i s t s .$
Commented by mr W last updated on 27/Feb/21

$a = \frac{1}{\frac{1}{18} - (\frac{1}{b} + \frac{1}{c})} \to 18 i f b, c \to + \infty$ $a = \frac{1}{\frac{1}{18} - (\frac{1}{b} + \frac{1}{c})} \to - \infty i f b, c \to 0^{+}$
	Answered by bramlexs22 last updated on 27/Feb/21

	$AM - GM$ $\frac{\frac{1}{a} + \frac{1}{b} + \frac{1}{c}}{3} ⩾ \sqrt[3]{\frac{1}{abc}}$ $\frac{[\frac{1}{18}]}{3} ⩾ \sqrt[3]{\frac{1}{abc}} \Rightarrow \frac{1}{54} ⩾ \sqrt[3]{\frac{1}{abc}}$ $\frac{1}{54^{3}} ⩾ \frac{1}{abc}, it hold for a = b = c$ $we get a = 54$
	Commented by mr W last updated on 27/Feb/21

	$w h a t d o y o u g e t i f b = c = 1000000 ?$ $w h a t d o y o u g e t i f b = c = 1 / 1000000 ?$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum