
Question and Answers Forum
Question Number 64762 by Lontum Hans-Sandys last updated on 21/Jul/19

Commented by mathmax by abdo last updated on 21/Jul/19
![1)g(x) =(a/(x+1)) +((bx+c)/(3x^2 +1)) a =lim_(x→−1) (x+1)g(x) =(1/2) lim_(x→+∞) xg(x) =0 =a+(b/3) ⇒3a+b =0 ⇒b=−(3/2) ⇒ g(x) =(1/(2(x+1))) −(1/2) ((3x−2c)/(3x^2 +1)) g(0) =2 =(1/2) +c ⇒c =2−(1/2) =(3/2) ⇒g(x) =(1/(2(x+1)))−(1/2)((3x−3)/(3x^2 +1)) b) ∫_0 ^1 g(x)dx =(1/2) ∫_0 ^1 (dx/(x+1)) −(1/2) ∫_0 ^1 ((x−1)/((x^2 +(1/3))))dx ∫_0 ^1 (dx/(x+1)) =[ln∣x+1∣]_0 ^1 =ln(2) ∫_0 ^1 ((x−1)/(x^2 +(1/3)))dx =(1/2) ∫_0 ^1 ((2x)/(x^2 +(1/3)))dx −∫_0 ^1 (dx/(x^2 +(1/3))) =[ln(x^2 +(1/3))]_0 ^1 −∫_0 ^1 (dx/(x^2 +(1/3))) =ln((4/3))−ln((1/3))−∫_0 ^1 (dx/(x^2 +(1/3))) =2ln(2)−∫_0 ^1 (dx/(x^2 +(1/3))) but we have ∫_0 ^1 (dx/(x^2 +(1/3))) =_(x =(t/(√3))) =∫_0 ^(√3) (dt/(((√3)/3)(1+t^2 ))) =(√3)[ arctan(t)]_0 ^(√3) =(√3) arctan((√3))=((π(√3))/3) ⇒ ∫_0 ^1 g(x)dx =((ln(2))/2) −(1/2){2ln(2)−((π(√3))/3)} =−((ln(2))/2) +((π(√3))/6)](Q64786.png)
Answered by Tanmay chaudhury last updated on 21/Jul/19
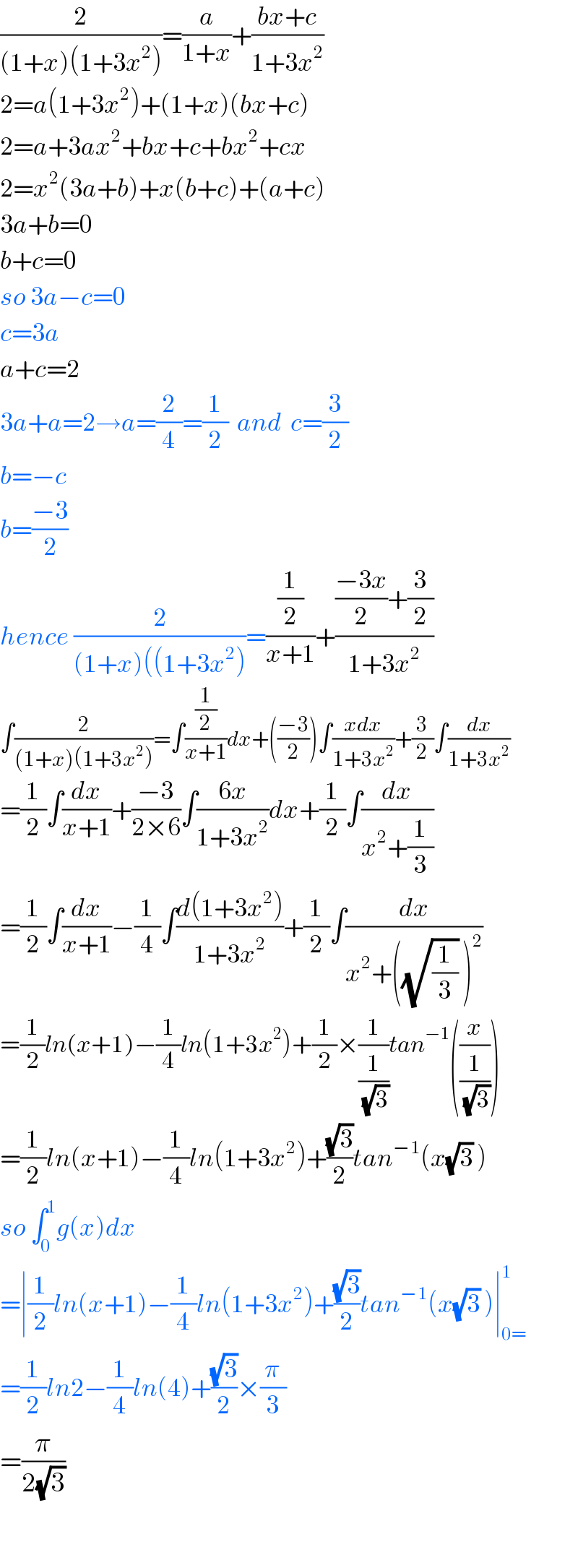
| ||
Question and Answers Forum | ||
Question Number 64762 by Lontum Hans-Sandys last updated on 21/Jul/19 | ||
 | ||
Commented by mathmax by abdo last updated on 21/Jul/19 | ||
![1)g(x) =(a/(x+1)) +((bx+c)/(3x^2 +1)) a =lim_(x→−1) (x+1)g(x) =(1/2) lim_(x→+∞) xg(x) =0 =a+(b/3) ⇒3a+b =0 ⇒b=−(3/2) ⇒ g(x) =(1/(2(x+1))) −(1/2) ((3x−2c)/(3x^2 +1)) g(0) =2 =(1/2) +c ⇒c =2−(1/2) =(3/2) ⇒g(x) =(1/(2(x+1)))−(1/2)((3x−3)/(3x^2 +1)) b) ∫_0 ^1 g(x)dx =(1/2) ∫_0 ^1 (dx/(x+1)) −(1/2) ∫_0 ^1 ((x−1)/((x^2 +(1/3))))dx ∫_0 ^1 (dx/(x+1)) =[ln∣x+1∣]_0 ^1 =ln(2) ∫_0 ^1 ((x−1)/(x^2 +(1/3)))dx =(1/2) ∫_0 ^1 ((2x)/(x^2 +(1/3)))dx −∫_0 ^1 (dx/(x^2 +(1/3))) =[ln(x^2 +(1/3))]_0 ^1 −∫_0 ^1 (dx/(x^2 +(1/3))) =ln((4/3))−ln((1/3))−∫_0 ^1 (dx/(x^2 +(1/3))) =2ln(2)−∫_0 ^1 (dx/(x^2 +(1/3))) but we have ∫_0 ^1 (dx/(x^2 +(1/3))) =_(x =(t/(√3))) =∫_0 ^(√3) (dt/(((√3)/3)(1+t^2 ))) =(√3)[ arctan(t)]_0 ^(√3) =(√3) arctan((√3))=((π(√3))/3) ⇒ ∫_0 ^1 g(x)dx =((ln(2))/2) −(1/2){2ln(2)−((π(√3))/3)} =−((ln(2))/2) +((π(√3))/6)](Q64786.png) | ||
Answered by Tanmay chaudhury last updated on 21/Jul/19 | ||
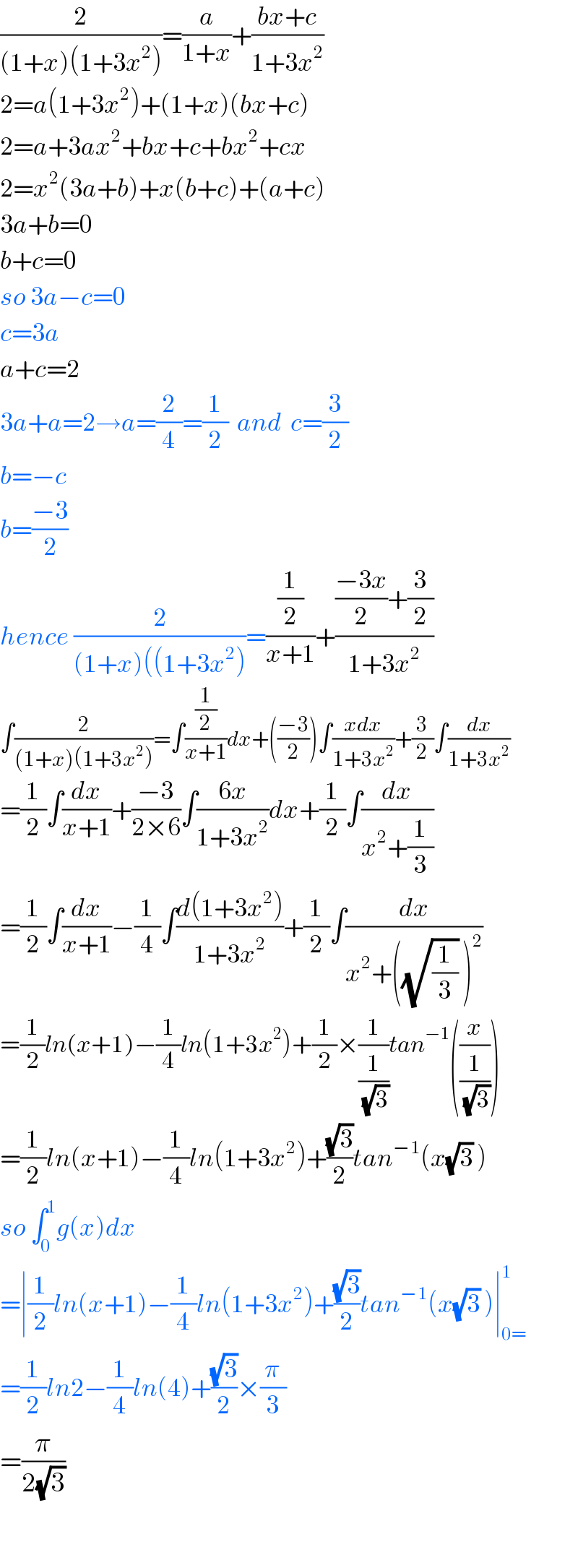 | ||
| ||