
Question and Answers Forum
Question Number 98443 by Ar Brandon last updated on 14/Jun/20
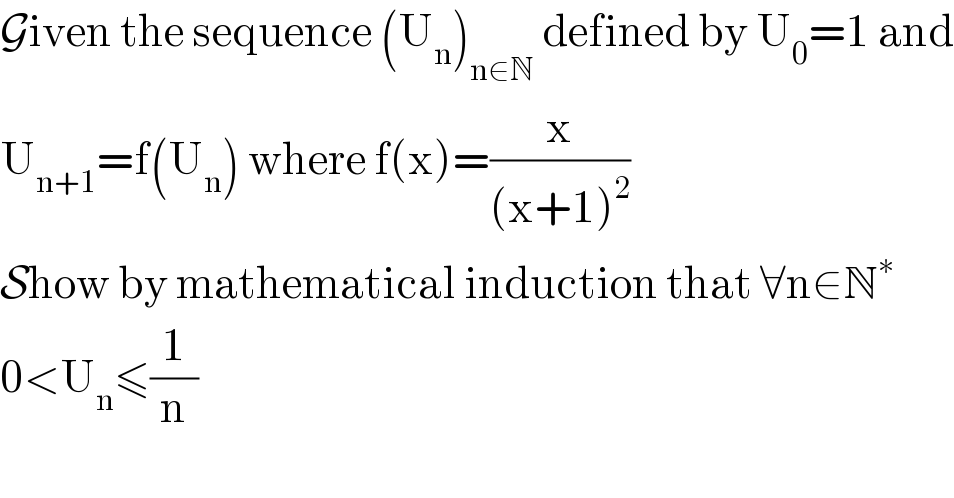
Answered by maths mind last updated on 14/Jun/20
![f(x)=(1/(x+1))−(1/((x+1)^2 )) f′(x)=−(1/((x+1)^2 ))+(2/((x+1)^3 ))=((1−x)/((1+x)^3 ))≥0 ,∀x∈[0,1] 0<U_0 =1≤1 true we assume That ∀n∈N 0<U_n ≤(1/n)≤1 since f is increasing over [0,1]⇒ ⇒f(0)<f(u_n )≤f((1/n)) ⇔0<U_(n+1) ≤(n/((n+1)^2 ))=(n/(n+1)).(1/(n+1))≤1.(1/(n+1))=(1/(n+1)) ⇒∀n∈N 0<U_n ≤(1/n)](Q98497.png)
Commented by Ar Brandon last updated on 14/Jun/20
Thank you ��
| ||
Question and Answers Forum | ||
Question Number 98443 by Ar Brandon last updated on 14/Jun/20 | ||
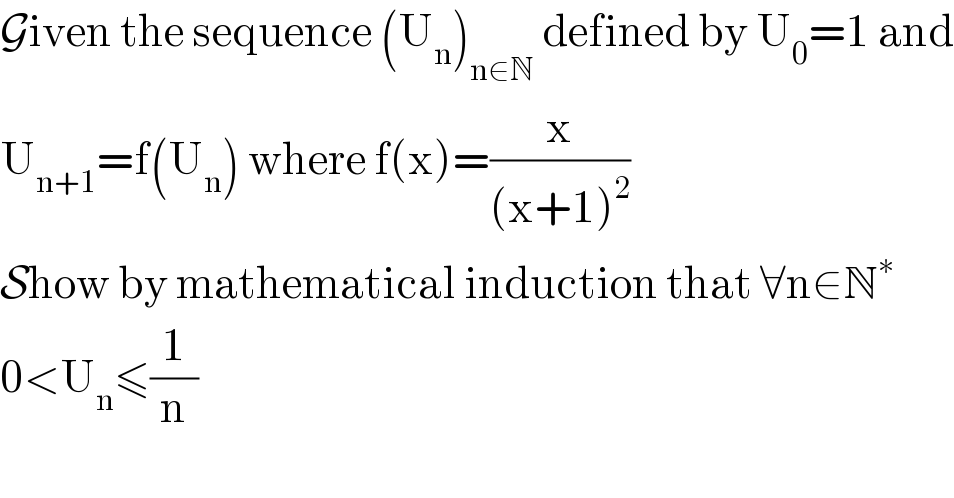 | ||
Answered by maths mind last updated on 14/Jun/20 | ||
![f(x)=(1/(x+1))−(1/((x+1)^2 )) f′(x)=−(1/((x+1)^2 ))+(2/((x+1)^3 ))=((1−x)/((1+x)^3 ))≥0 ,∀x∈[0,1] 0<U_0 =1≤1 true we assume That ∀n∈N 0<U_n ≤(1/n)≤1 since f is increasing over [0,1]⇒ ⇒f(0)<f(u_n )≤f((1/n)) ⇔0<U_(n+1) ≤(n/((n+1)^2 ))=(n/(n+1)).(1/(n+1))≤1.(1/(n+1))=(1/(n+1)) ⇒∀n∈N 0<U_n ≤(1/n)](Q98497.png) | ||
| ||
Commented by Ar Brandon last updated on 14/Jun/20 | ||
Thank you �� | ||