
Question and Answers Forum
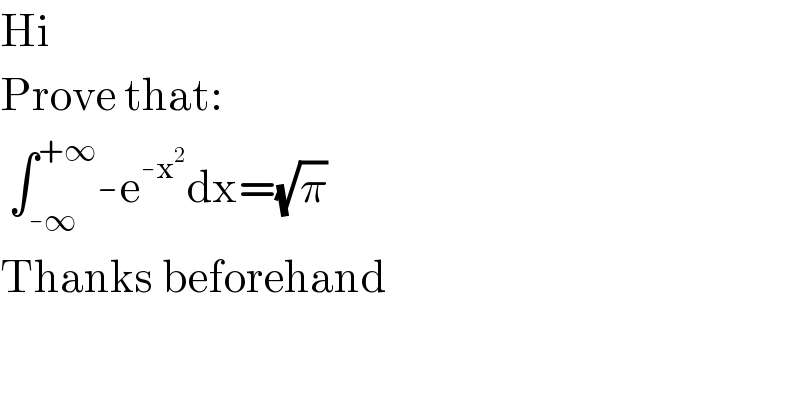
Question Number 116806 by Backer last updated on 07/Oct/20
Answered by Bird last updated on 07/Oct/20
![let A_ξ =∫∫_(]−ξ,ξ[^2 ) e^(−x^2 −y^2 ) dxdy we hsve lim_(ξ→+∞) A_ξ =(∫_(−∞) ^∞ e^(−x^2 ) dx)^2 let use the diffeomorphism { ((x =rcosθ)),((y =rsinθ we have −ξ≤x≤ξ)) :} and −ξ≤y≤ξ ⇒0≤x^2 +y^2 ≤2ξ^2 ⇒0≤r≤ξ(√2) ⇒ A_ξ =∫_0 ^(ξ(√2)) r e^(−r^2 ) dr ∫_(−π) ^π dθ =2π [−(1/2)e^(−r^2 ) ]_0 ^(ξ(√2)) =π(1−e^(−2ξ^2 ) ) ⇒lim_(ξ→+∞) A_ξ =π =(∫_(−∞) ^(+∞) e^(−x^2 ) dx)^2 but∫_(−∞) ^∞ e^(−x^2 ) dx>0 ⇒∫_(−∞) ^(+∞) e^(−x^2 ) dx =(√π)](Q116807.png)
Answered by bobhans last updated on 07/Oct/20
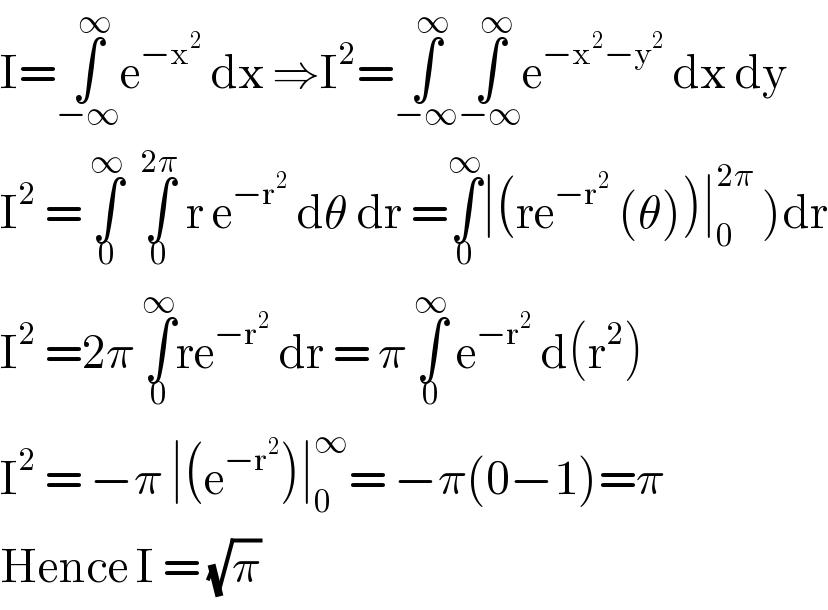
| ||
Question and Answers Forum | ||
Question Number 116806 by Backer last updated on 07/Oct/20 | ||
 | ||
Answered by Bird last updated on 07/Oct/20 | ||
![let A_ξ =∫∫_(]−ξ,ξ[^2 ) e^(−x^2 −y^2 ) dxdy we hsve lim_(ξ→+∞) A_ξ =(∫_(−∞) ^∞ e^(−x^2 ) dx)^2 let use the diffeomorphism { ((x =rcosθ)),((y =rsinθ we have −ξ≤x≤ξ)) :} and −ξ≤y≤ξ ⇒0≤x^2 +y^2 ≤2ξ^2 ⇒0≤r≤ξ(√2) ⇒ A_ξ =∫_0 ^(ξ(√2)) r e^(−r^2 ) dr ∫_(−π) ^π dθ =2π [−(1/2)e^(−r^2 ) ]_0 ^(ξ(√2)) =π(1−e^(−2ξ^2 ) ) ⇒lim_(ξ→+∞) A_ξ =π =(∫_(−∞) ^(+∞) e^(−x^2 ) dx)^2 but∫_(−∞) ^∞ e^(−x^2 ) dx>0 ⇒∫_(−∞) ^(+∞) e^(−x^2 ) dx =(√π)](Q116807.png) | ||
| ||
Answered by bobhans last updated on 07/Oct/20 | ||
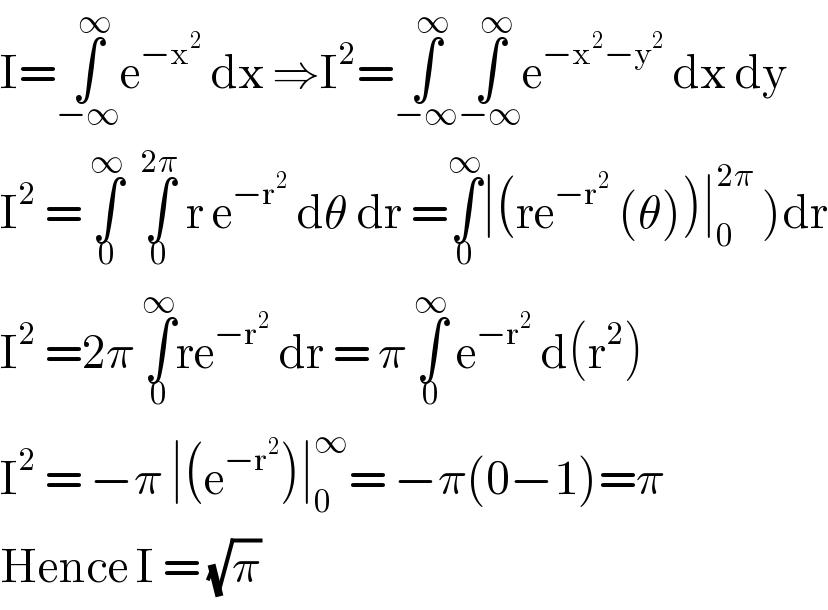 | ||
| ||