
Question and Answers Forum
Question Number 55520 by Rdk96 last updated on 26/Feb/19
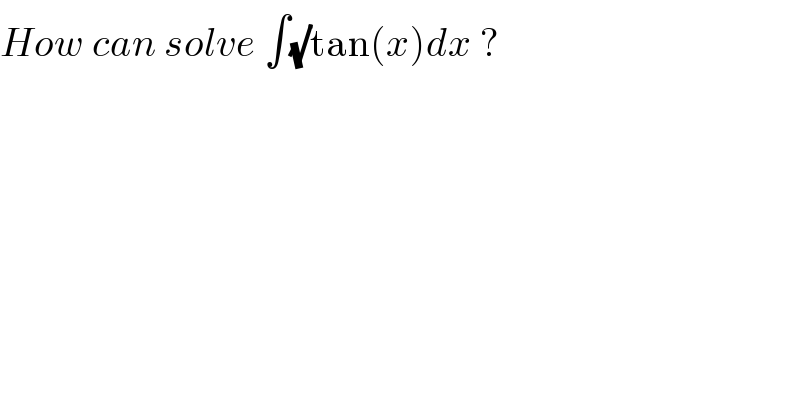
Commented by maxmathsup by imad last updated on 26/Feb/19

Commented by maxmathsup by imad last updated on 26/Feb/19
Answered by tanmay.chaudhury50@gmail.com last updated on 26/Feb/19

Commented by Rdk96 last updated on 26/Feb/19
Commented by tanmay.chaudhury50@gmail.com last updated on 26/Feb/19
Commented by Rdk96 last updated on 26/Feb/19

Answered by tanmay.chaudhury50@gmail.com last updated on 26/Feb/19
![or method... p=∫(√(tanx)) +(√(cotx)) dx q=(√(tanx)) −(√(cotx)) dx ∫(√(tanx)) dx=((p+q)/2) p=∫(√((sinx)/(cosx))) +(√((cosx)/(sinx))) dx p=∫((sinx+cosx)/(√(sinxcosx)))dx p=(√2)∫((d(sinx−cosx))/(√(1−1+2sinxcosx)))dx =(√2) ∫((d(sinx−cosx))/((√(1−(sinx−cosx)^2 )) )) =(√2) sin^(−1) (sinx−cosx) +c_1 q=∫((√((sinx)/(cosx))) −(√((cosx)/(sinx))) ) dx q=∫((sinx−cosx)/(√(sinxcosx)))dx→−∫((cosx−sinx)/(√(sinxcosx)))dx q=(−(√2) )∫((d(sinx+cosx))/(√(1+2sinxcosx−1))) =(−(√2) )∫((d(sinx+cosx))/(√((sinx+cosx)^2 −1))) =(−(√2) )ln{(sinx+cosx)+(√((sinx+cosx)^2 −1)) } so ∫(√(tanx)) dx ((√2)/2)[sin^(−1) (sinx−cosx)−ln{(sinx+cosx)+(√((sinx+cosx)^2 −1)) }]+c pls check...](Q55525.png)
Answered by MJS last updated on 26/Feb/19
![∫(√(tan x))dx= [t=(√(tan x)) → dx=2cos^2 x (√(tan x))dt=((2tdt)/(t^4 +1))] =2∫(t^2 /(t^4 +1))dt=2∫(t^2 /((t^2 −(√2)t+1)(t^2 +(√2)t+1)))dt= =2∫((((√2)t)/(4(t^2 −(√2)t+1)))−(((√2)t)/(4(t^2 +(√2)t+1))))dt= =(1/2)∫((((√2)t−1)/(t^2 −(√2)t+1))+(1/(t^2 −(√2)t+1))−(((√2)t+1)/(t^2 +(√2)t+1))+(1/(t^2 +(√2)t+1)))dt= =((√2)/4)∫(((2t−(√2))/(t^2 −(√2)t+1))−((2t+(√2))/(t^2 +(√2)t+1)))dt+(1/2)∫((1/(t^2 −(√2)t+1))+(1/(t^2 +(√2)t+1)))dt= =((√2)/4)(ln (t^2 −(√2)t+1) −ln (t^2 +(√2)t+1))+((√2)/2)(arctan ((√2)t−1) +arctan ((√2)t+1))= =((√2)/4)(ln ∣((tan x −(√(2tan x))+1)/(tan x +(√(2tan x))+1))∣ +2(arctan ((√(2tan x))−1) +arctan ((√(2tan x))+1)))+C](Q55529.png)
Commented by behi83417@gmail.com last updated on 26/Feb/19
![arctg((√(2tgx))−1)+arctg((√(2tgx))+1)= arctg((2(√(2tgx)))/(2(1−tgx)))=arctg(((√(2tgx))/(1−tgx)))= arccos∣cosx−sinx∣ ln((tgx−(√(2tgx))+1)/(tgx+(√(2tgx))+1))=ln(((tgx+1−(√(2tgx)))^2 )/(tg^2 x+1))= =2ln[cosx.(tgx+1−(√(2tgx))]= =2ln[sinx+cosx−(√(sin2x))] ⇒I=((√2)/2).ln∣cosx+sinx−(√(sin2x))∣+2cos^(−1) ∣cosx−sinx∣+C](Q55530.png)
Commented by MJS last updated on 26/Feb/19

