
Question and Answers Forum
Question Number 162604 by amin96 last updated on 30/Dec/21
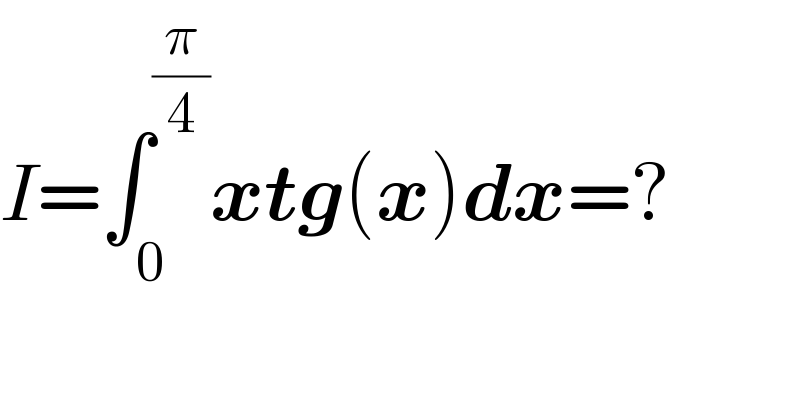
Answered by Ar Brandon last updated on 30/Dec/21
![I=∫_0 ^(π/4) xtanxdx =−[xln(cosx)]_0 ^(π/4) +∫_0 ^(π/4) ln(cosx)dx =−(π/4)ln((1/( (√2))))+(G/2)−((πln2)/4)=(G/2)−((πln2)/8)](Q162609.png)
| ||
Question and Answers Forum | ||
Question Number 162604 by amin96 last updated on 30/Dec/21 | ||
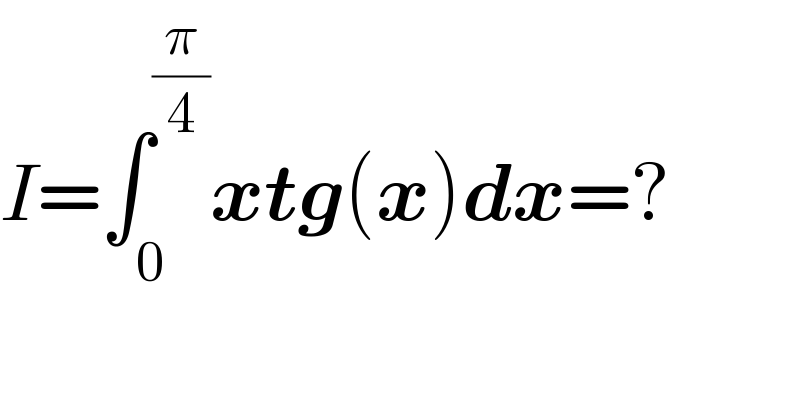 | ||
Answered by Ar Brandon last updated on 30/Dec/21 | ||
![I=∫_0 ^(π/4) xtanxdx =−[xln(cosx)]_0 ^(π/4) +∫_0 ^(π/4) ln(cosx)dx =−(π/4)ln((1/( (√2))))+(G/2)−((πln2)/4)=(G/2)−((πln2)/8)](Q162609.png) | ||
| ||