
Question and Answers Forum
Question Number 137187 by mathocean1 last updated on 30/Mar/21
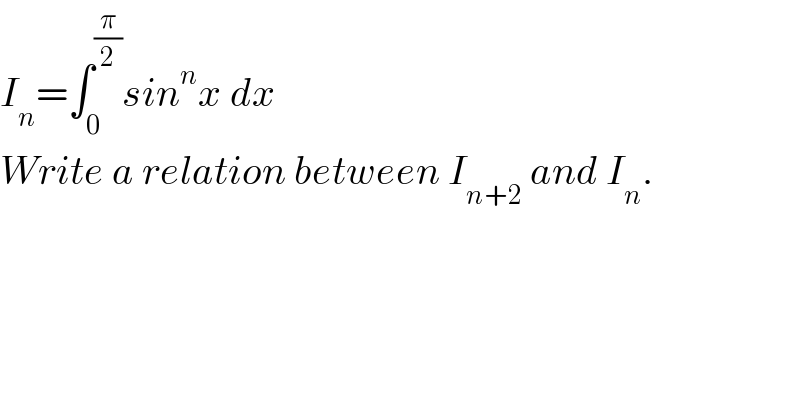
Answered by Dwaipayan Shikari last updated on 30/Mar/21
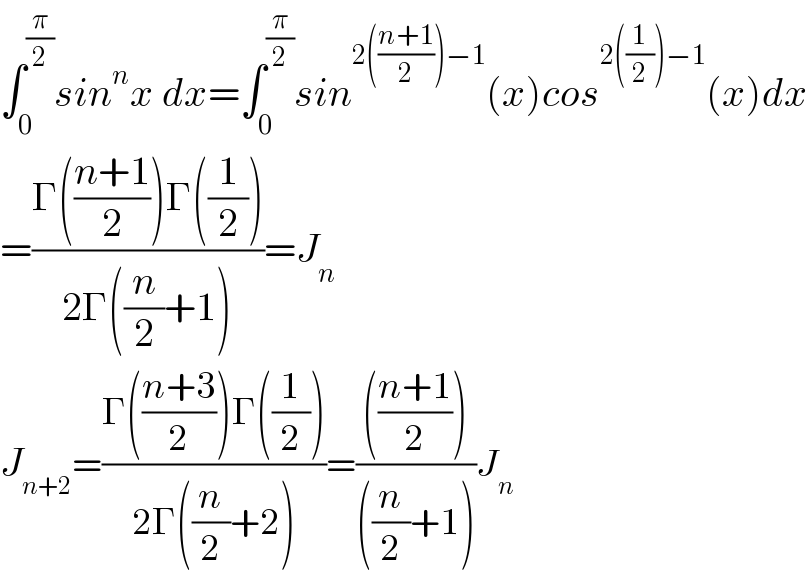
Answered by mathmax by abdo last updated on 30/Mar/21
![I_(n+2) =∫_0 ^(π/2) sin^n x sin^2 xdx =∫_0 ^(π/2) sin^n x(1−cos^2 x)dx =∫_0 ^(π/2) sin^n xdx −∫_0 ^(π/2) cos^2 x sin^n x dx=I_n −J J =∫_0 ^(π/2) cosx(cosx sin^n x)dx =_(by parts) [((sin^(n+1) x)/(n+1))cosx]_0 ^(π/2) −∫_0 ^(π/2) (−sinx)((sin^(n+1) x)/(n+1))dx =(1/(n+1))∫_0 ^(π/2) sin^(n+2) xdx ⇒I_(n+2 ) =I_n −(1/(n+1))I_(n+2) ⇒ (1+(1/(n+1)))I_(n+2) =I_n ⇒((n+2)/(n+1))I_(n+2) =I_n ⇒I_(n+2) =((n+1)/(n+2))I_n](Q137199.png)
| ||
Question and Answers Forum | ||
Question Number 137187 by mathocean1 last updated on 30/Mar/21 | ||
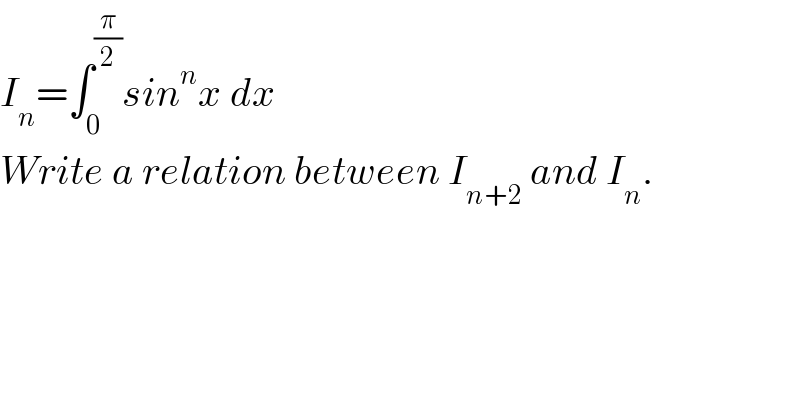 | ||
Answered by Dwaipayan Shikari last updated on 30/Mar/21 | ||
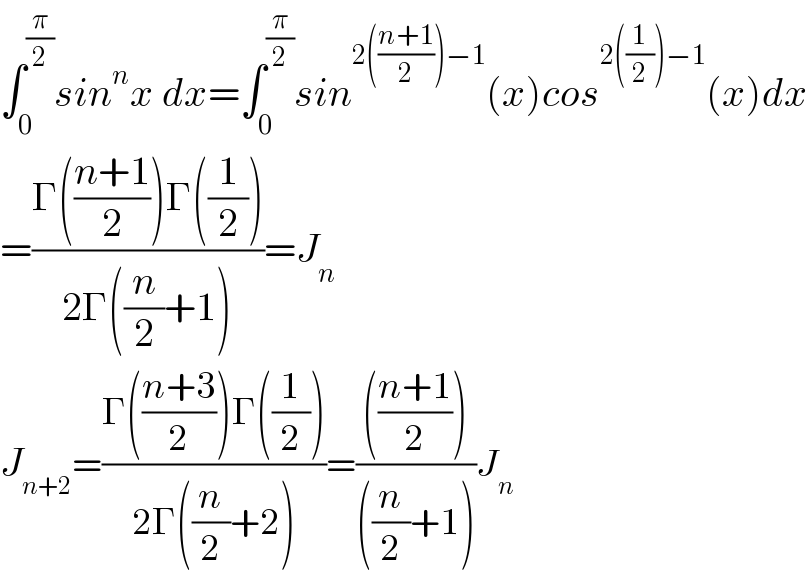 | ||
| ||
Answered by mathmax by abdo last updated on 30/Mar/21 | ||
![I_(n+2) =∫_0 ^(π/2) sin^n x sin^2 xdx =∫_0 ^(π/2) sin^n x(1−cos^2 x)dx =∫_0 ^(π/2) sin^n xdx −∫_0 ^(π/2) cos^2 x sin^n x dx=I_n −J J =∫_0 ^(π/2) cosx(cosx sin^n x)dx =_(by parts) [((sin^(n+1) x)/(n+1))cosx]_0 ^(π/2) −∫_0 ^(π/2) (−sinx)((sin^(n+1) x)/(n+1))dx =(1/(n+1))∫_0 ^(π/2) sin^(n+2) xdx ⇒I_(n+2 ) =I_n −(1/(n+1))I_(n+2) ⇒ (1+(1/(n+1)))I_(n+2) =I_n ⇒((n+2)/(n+1))I_(n+2) =I_n ⇒I_(n+2) =((n+1)/(n+2))I_n](Q137199.png) | ||
| ||