
Question and Answers Forum
Question Number 68351 by mhmd last updated on 09/Sep/19
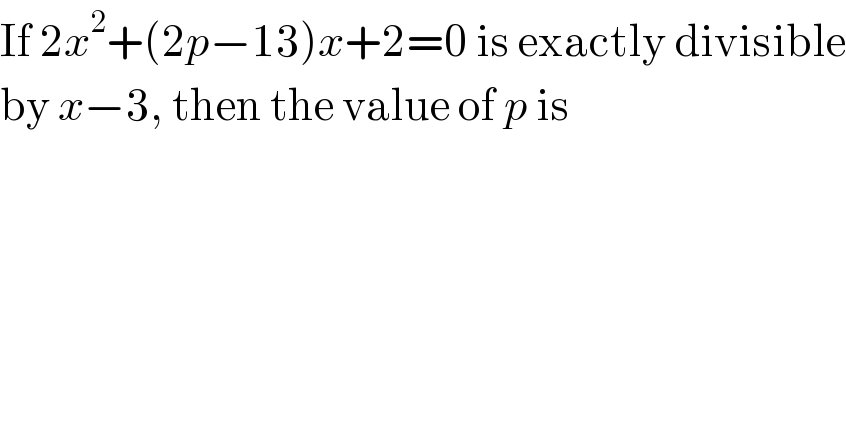
Answered by $@ty@m123 last updated on 09/Sep/19
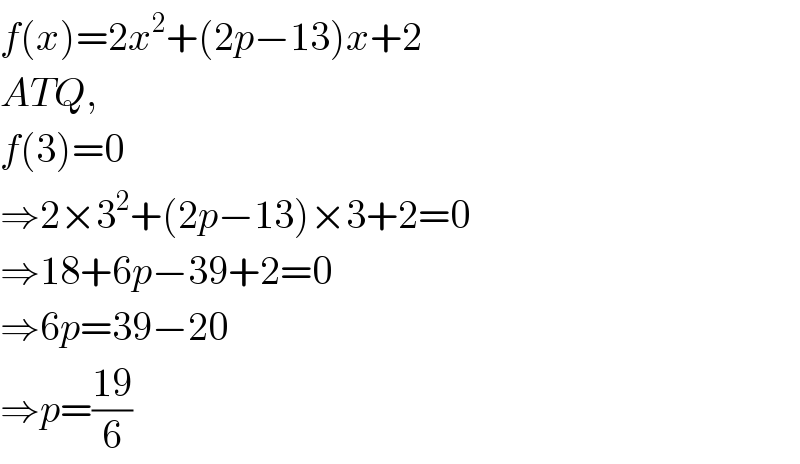
Answered by Rasheed.Sindhi last updated on 10/Sep/19
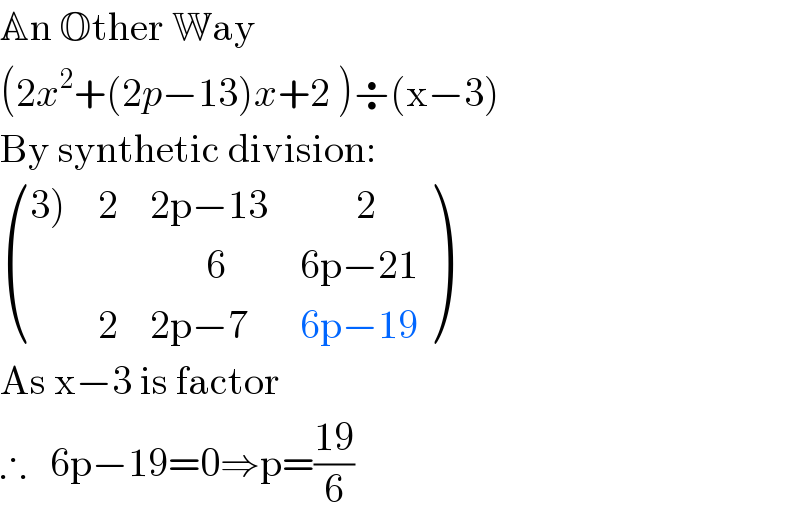
| ||
Question and Answers Forum | ||
Question Number 68351 by mhmd last updated on 09/Sep/19 | ||
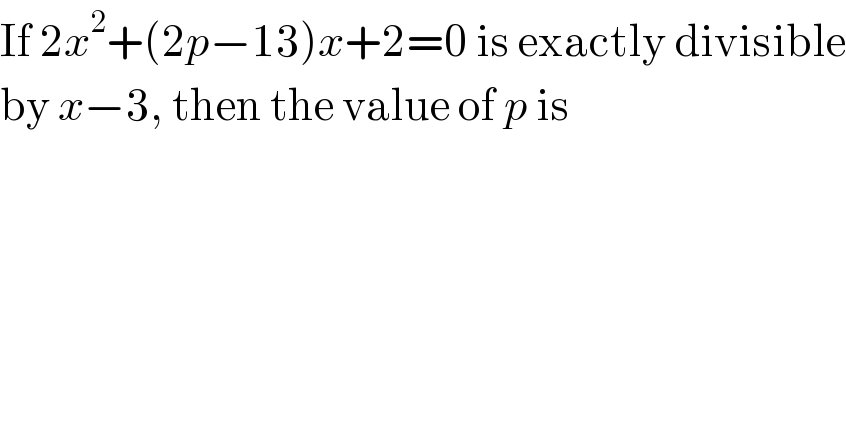 | ||
Answered by $@ty@m123 last updated on 09/Sep/19 | ||
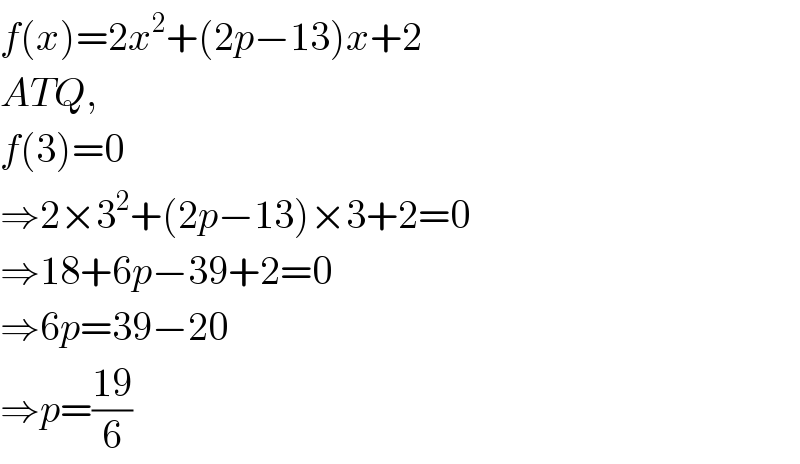 | ||
| ||
Answered by Rasheed.Sindhi last updated on 10/Sep/19 | ||
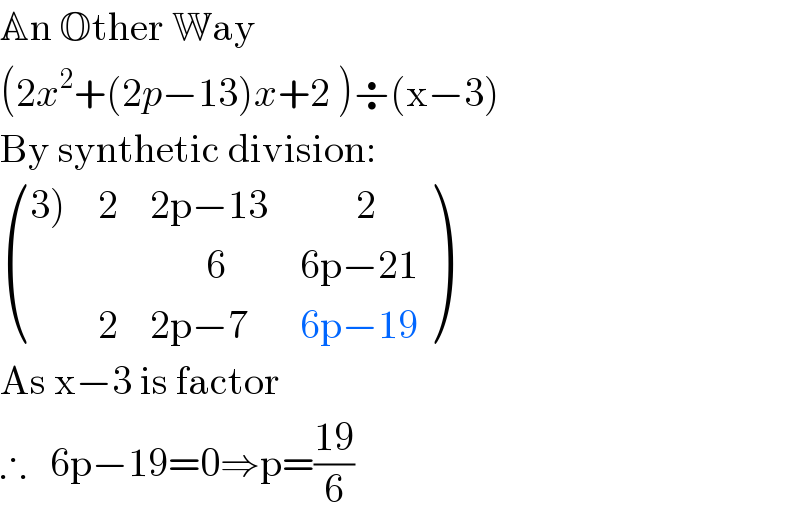 | ||
| ||