
Question and Answers Forum
Question Number 178818 by Shrinava last updated on 21/Oct/22
![If a,b,c,d∈[1,2] then prove that: (a + b + c + d + e)((1/a) + (1/b) + (1/c) + (1/d) + (1/e)) ≤ 28 When equality holds?](Q178818.png)
Answered by mr W last updated on 22/Oct/22
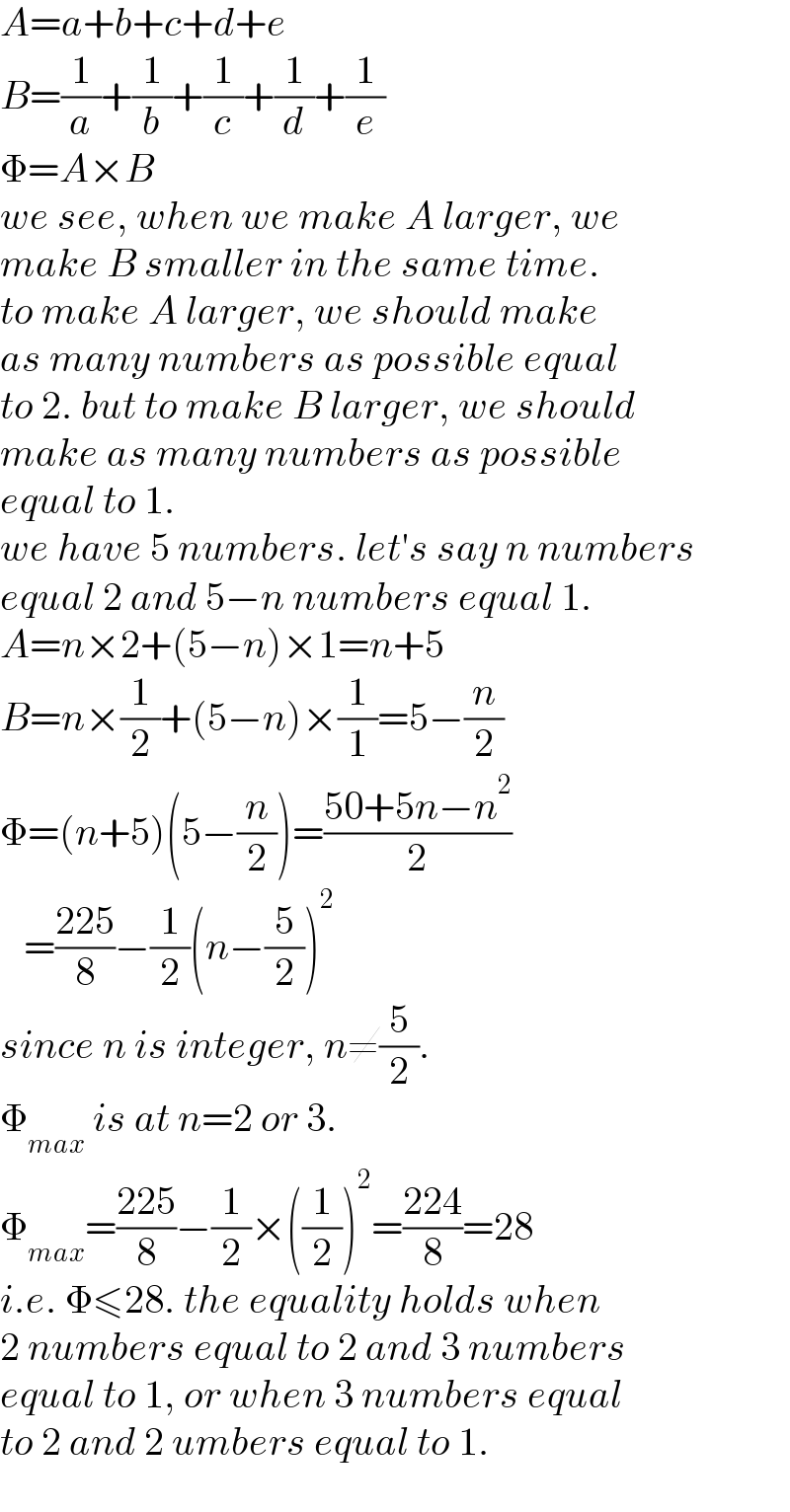
Commented by Tawa11 last updated on 22/Oct/22

Commented by Shrinava last updated on 23/Oct/22
| ||
Question and Answers Forum | ||
Question Number 178818 by Shrinava last updated on 21/Oct/22 | ||
![If a,b,c,d∈[1,2] then prove that: (a + b + c + d + e)((1/a) + (1/b) + (1/c) + (1/d) + (1/e)) ≤ 28 When equality holds?](Q178818.png) | ||
Answered by mr W last updated on 22/Oct/22 | ||
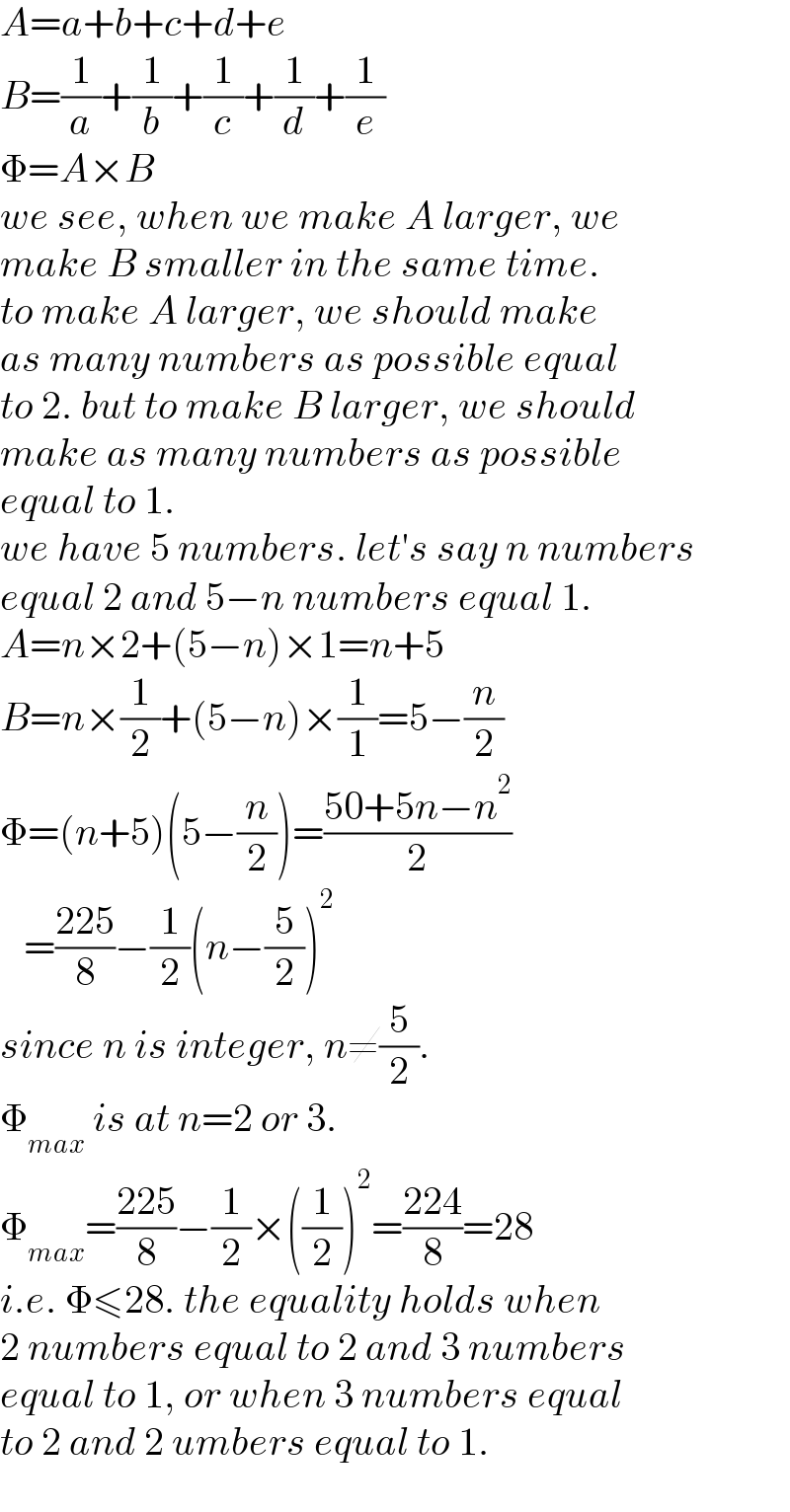 | ||
| ||
Commented by Tawa11 last updated on 22/Oct/22 | ||
 | ||
Commented by Shrinava last updated on 23/Oct/22 | ||
 | ||