Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 10955 by Joel576 last updated on 04/Mar/17

$$\mathrm{If}\frac{\cos \theta }{1-\sin \theta }=aa\ne \frac{\pi }{2}+2k\pi$$$$\mathrm{So},\tan \frac{\theta }{2}=...$$$$\left(\mathrm{A}\right)\frac{a}{a+1}\left(\mathrm{D}\right)\frac{a+1}{a-1}$$$$\left(\mathrm{B}\right)\frac{1}{a+1}\left(\mathrm{E}\right)\frac{a}{a-1}$$$$\left(\mathrm{C}\right)\frac{a-1}{a+1}$$

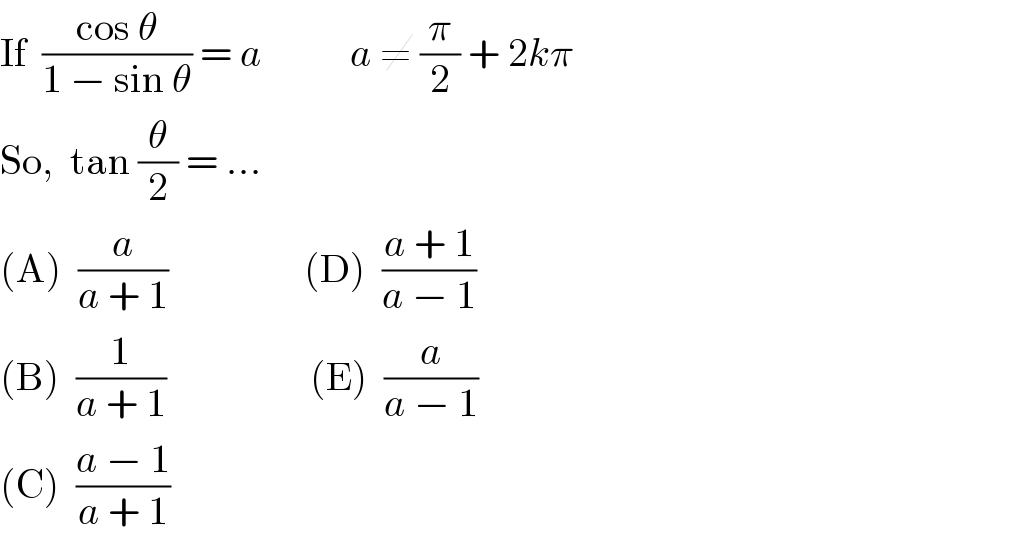
Answered by ajfour last updated on 04/Mar/17

$$$$$$\frac{\sin (\frac{\pi }{2}-\theta )}{1-\cos (\frac{\pi }{2}-\theta )}=\frac{2\sin (\frac{\pi }{4}-\frac{\theta }{2})\cos (\frac{\pi }{4}-\frac{\theta }{2})}{2\sin {}^2(\frac{\pi }{4}-\frac{\theta }{2})}$$$$=\cot (\frac{\pi }{4}-\frac{\theta }{2})=a$$$$\tan (\frac{\pi }{4}-\frac{\theta }{2})=\frac{1}{a};let\tan \left(\frac{\theta }{2}\right)=p$$$$\frac{1-p}{1+p}=\frac{1}{a}\Rightarrow a-ap=1+p$$$$p=\frac{a-1}{a+1}.$$

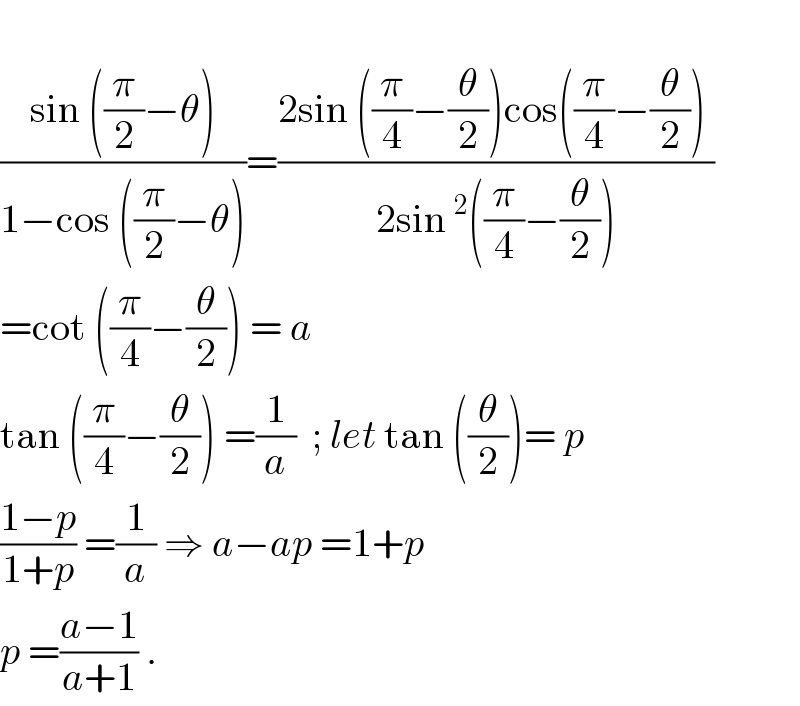
Commented by Joel576 last updated on 05/Mar/17

$$thankyouverymuch$$

Answered by ridwan balatif last updated on 04/Mar/17

$$\mathrm{another}\mathrm{way}$$$${\left(\frac{\cos \theta }{1-\sin \theta }\right)}^2={\left(\mathrm{a}\right)}^2$$$$\frac{{\cos }^2\theta }{{(1-\sin \theta )}^2}={\mathrm{a}}^2$$$$\frac{(1-{\sin }^2\theta )}{{(1-\sin \theta )}^2}={\mathrm{a}}^2$$$$\frac{(1-\sin \theta )(1+\sin \theta )}{(1-\sin \theta )(1-\sin \theta )}={\mathrm{a}}^2$$$$\frac{1+\sin \theta }{1-\sin \theta }={\mathrm{a}}^2$$$$\sin \theta =\frac{{\mathrm{a}}^2-1}{{\mathrm{a}}^2+1}$$$$\cos \theta =\frac{2\mathrm{a}}{{\mathrm{a}}^2+1}$$$$\mathrm{remember}:\tan \frac{\theta }{2}=\frac{\sin \theta }{1+\cos \theta }$$$$\tan \frac{\theta }{2}=\frac{\frac{{\mathrm{a}}^2-1}{{\mathrm{a}}^2+1}}{1+\frac{2\mathrm{a}}{{\mathrm{a}}^2+1}}$$$$\tan \frac{\theta }{2}=\frac{\frac{{\mathrm{a}}^2-1}{{\mathrm{a}}^2+1}}{\frac{{\mathrm{a}}^2+2\mathrm{a}+1}{{\mathrm{a}}^2+1}}$$$$\tan \frac{\theta }{2}=\frac{{\mathrm{a}}^2-1}{{\mathrm{a}}^2+2\mathrm{a}+1}$$$$\tan \frac{\theta }{2}=\frac{(\mathrm{a}-1)(\mathrm{a}+1)}{{(\mathrm{a}+1)}^2}$$$$\tan \frac{\theta }{2}=\frac{\mathrm{a}-1}{\mathrm{a}+1}$$$$\mathrm{Answer}:\left(\mathrm{C}\right)$$

Commented by Joel576 last updated on 05/Mar/17

$$thankyouverymuch$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com