If Σ_(r=1) ^n t_r =((n(n+1)(n+2)(n+3))/8) then lim_(n→∞) Σ_(r=1) ^n (1/t


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 110173 by ajfour last updated on 27/Aug/20

$I f \underset{r = 1}{\sum^{n}} t_{r} = \frac{n (n + 1) (n + 2) (n + 3)}{8}$ $t h e n \lim_{n \to \infty} \underset{r = 1}{\sum^{n}} \frac{1}{t_{r}} = ?$
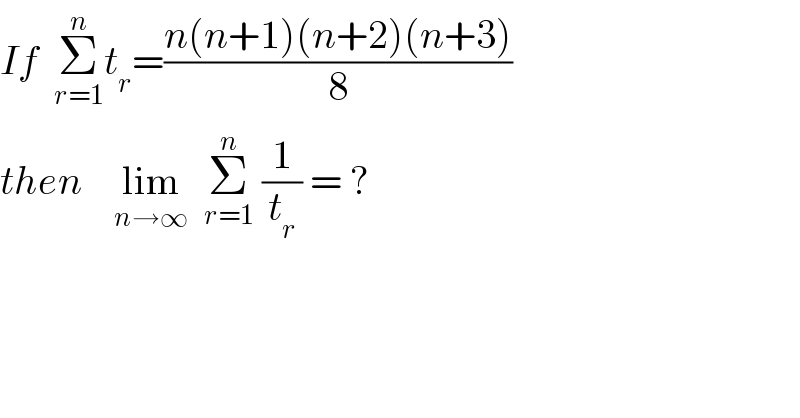
	Answered by Olaf last updated on 27/Aug/20

	$t_{n} = \underset{r = 1}{\sum^{n}} t_{r} - \underset{r = 1}{\sum^{n - 1}} t_{r}$ $t_{n} = \frac{n (n + 1) (n + 2) (n + 3)}{8} - \frac{(n - 1) n (n + 1) (n + 2)}{8}$ $t_{n} = \frac{n (n + 1) (n + 2) [n + 3 - n + 1]}{8}$ $t_{n} = \frac{n (n + 1) (n + 2)}{2}$ $t_{r} = \frac{r (r + 1) (r + 2)}{2}$ $\frac{1}{t_{r}} = \frac{2}{r (r + 1) (r + 2)} = \frac{1}{r} - \frac{2}{r + 1} + \frac{1}{r + 2}$ $\underset{r = 1}{\sum^{n}} \frac{1}{t_{r}} = \underset{r = 1}{\sum^{n}} \frac{1}{r} - 2 \underset{r = 1}{\sum^{n}} \frac{1}{r + 1} + \underset{r = 1}{\sum^{n}} \frac{1}{r + 2}$ $\underset{r = 1}{\sum^{n}} \frac{1}{t_{r}} = \underset{r = 1}{\sum^{n}} \frac{1}{r} - 2 \underset{r = 2}{\sum^{n + 1}} \frac{1}{r} + \underset{r = 3}{\sum^{n + 2}} \frac{1}{r}$ $\underset{r = 1}{\sum^{n}} \frac{1}{t_{r}} = \underset{r = 1}{\sum^{n}} \frac{1}{r} - 2 (\underset{r = 1}{\sum^{n}} \frac{1}{r} - 1 + \frac{1}{n + 1})$ $+ (\underset{r = 1}{\sum^{n}} \frac{1}{r} - 1 - \frac{1}{2} + \frac{1}{n + 1} + \frac{1}{n + 2})$ $\underset{r = 1}{\sum^{n}} \frac{1}{t_{r}} = 2 - \frac{2}{n + 1} - \frac{3}{2} + \frac{1}{n + 1} + \frac{1}{n + 2}$ $\underset{r = 1}{\sum^{n}} \frac{1}{t_{r}} = \frac{1}{2} - \frac{1}{n + 1} + \frac{1}{n + 2}$ $\underset{r = 1}{\sum^{n}} \frac{1}{t_{r}} = \frac{1}{2} - \frac{1}{(n + 1) (n + 2)}$ $\lim_{n \to \infty} \underset{r = 1}{\sum^{n}} \frac{1}{t_{r}} = \frac{1}{2}$
	Commented by ajfour last updated on 27/Aug/20

	$r i g h t a n s w e r, t h a n k s S i r .$
	Answered by Dwaipayan Shikari last updated on 27/Aug/20

	$△ \underset{r = 1}{\sum^{n}} t_{r} = \frac{n (n + 1) (n + 2) (n + 3)}{8} - \frac{(n - 1) n (n + 1) (n + 2)}{8}$ $t_{n} = \frac{n (n + 1) (n + 2)}{2}$ $\sum^{\infty} \frac{1}{t_{n}} = \sum^{\infty} \frac{2}{n (n + 1) (n + 2)} = \sum^{\infty} \frac{n + 2 - n}{n (n + 1) (n + 2)} = \sum^{\infty} \frac{1}{n} - \frac{1}{n + 1} - \sum^{\infty} \frac{1}{n + 1} - \frac{1}{n + 2}$ $= \lim_{n \to \infty} (1 - \frac{1}{n + 1}) - \lim_{n \to \infty} (\frac{1}{2} - \frac{1}{n + 2})$ $= 1 - \frac{1}{2} = \frac{1}{2}$
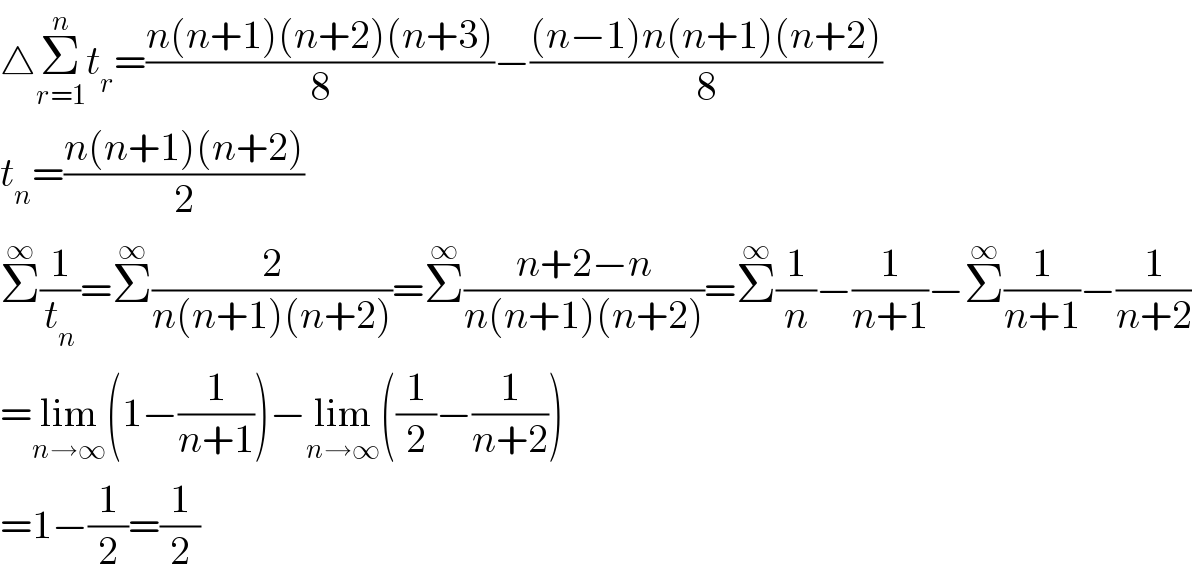
	Commented by ajfour last updated on 27/Aug/20

	$G r e a t w a y S i r; t h a n k s a l o t .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum