
Question and Answers Forum
Question Number 21247 by Tinkutara last updated on 17/Sep/17
![If [ ] represents the greatest integer function and f(x) = x − [x] then number of real roots of the equation f(x) + f((1/x)) = 1 are infinite. True/False](Q21247.png)
Answered by dioph last updated on 21/Sep/17
![x−[x] + (1/x)−[(1/x)] = 1 x = 1 is not a root. if x > 1, [(1/x)] = 0 and hence: x − [x] + (1/x) = 1 For some fixed [x]=k we have: x^2 −(k+1)x + 1 = 0 x = ((k+1±(√(k^2 +2k−3)))/2) k = 1 ⇒ x = 1 which we have already considered. k > 1 ⇒ 2k > 3 ⇒ k^2 < k^2 +2k−3 < (k+1)^2 ⇒ k+(1/2) < ((k+1+(√(k^2 +2k−3)))/2) < k+1 Hence there is one real root x for every k = [x] > 1 Because we have no further assumptions about k, the function does indeed have infinite real roots (True)](Q21358.png)
Commented by dioph last updated on 21/Sep/17
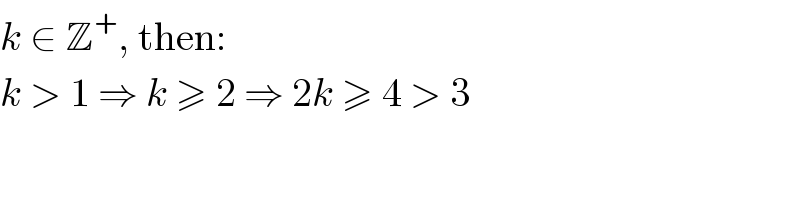
Commented by Tinkutara last updated on 22/Sep/17
| ||
Question and Answers Forum | ||
Question Number 21247 by Tinkutara last updated on 17/Sep/17 | ||
![If [ ] represents the greatest integer function and f(x) = x − [x] then number of real roots of the equation f(x) + f((1/x)) = 1 are infinite. True/False](Q21247.png) | ||
Answered by dioph last updated on 21/Sep/17 | ||
![x−[x] + (1/x)−[(1/x)] = 1 x = 1 is not a root. if x > 1, [(1/x)] = 0 and hence: x − [x] + (1/x) = 1 For some fixed [x]=k we have: x^2 −(k+1)x + 1 = 0 x = ((k+1±(√(k^2 +2k−3)))/2) k = 1 ⇒ x = 1 which we have already considered. k > 1 ⇒ 2k > 3 ⇒ k^2 < k^2 +2k−3 < (k+1)^2 ⇒ k+(1/2) < ((k+1+(√(k^2 +2k−3)))/2) < k+1 Hence there is one real root x for every k = [x] > 1 Because we have no further assumptions about k, the function does indeed have infinite real roots (True)](Q21358.png) | ||
| ||
Commented by dioph last updated on 21/Sep/17 | ||
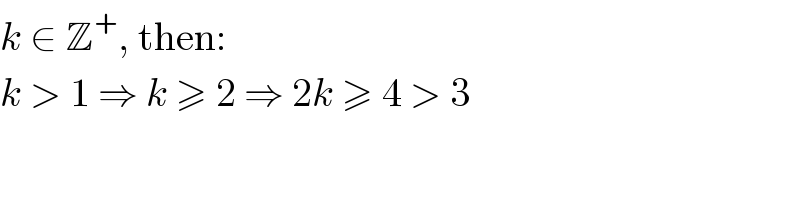 | ||
Commented by Tinkutara last updated on 22/Sep/17 | ||
 | ||