Integrate..∫(√(1+(√(1+(√x))))) dx


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 55873 by Easyman32 last updated on 05/Mar/19

$I n t e g r a t e . . \int \sqrt{1 + \sqrt{1 + \sqrt{x}}} d x$
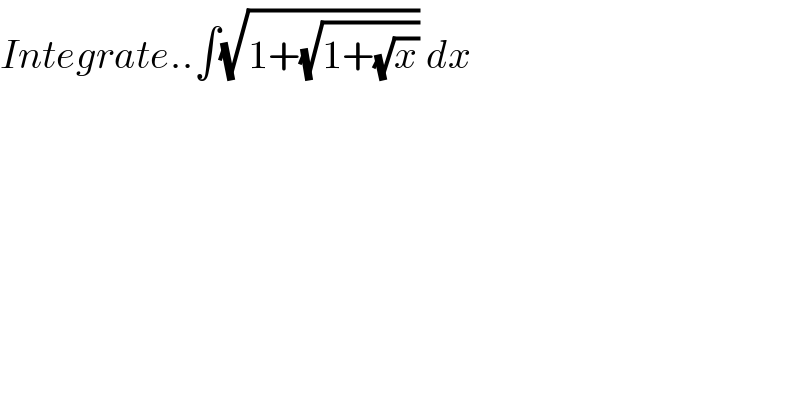
Commented by maxmathsup by imad last updated on 05/Mar/19
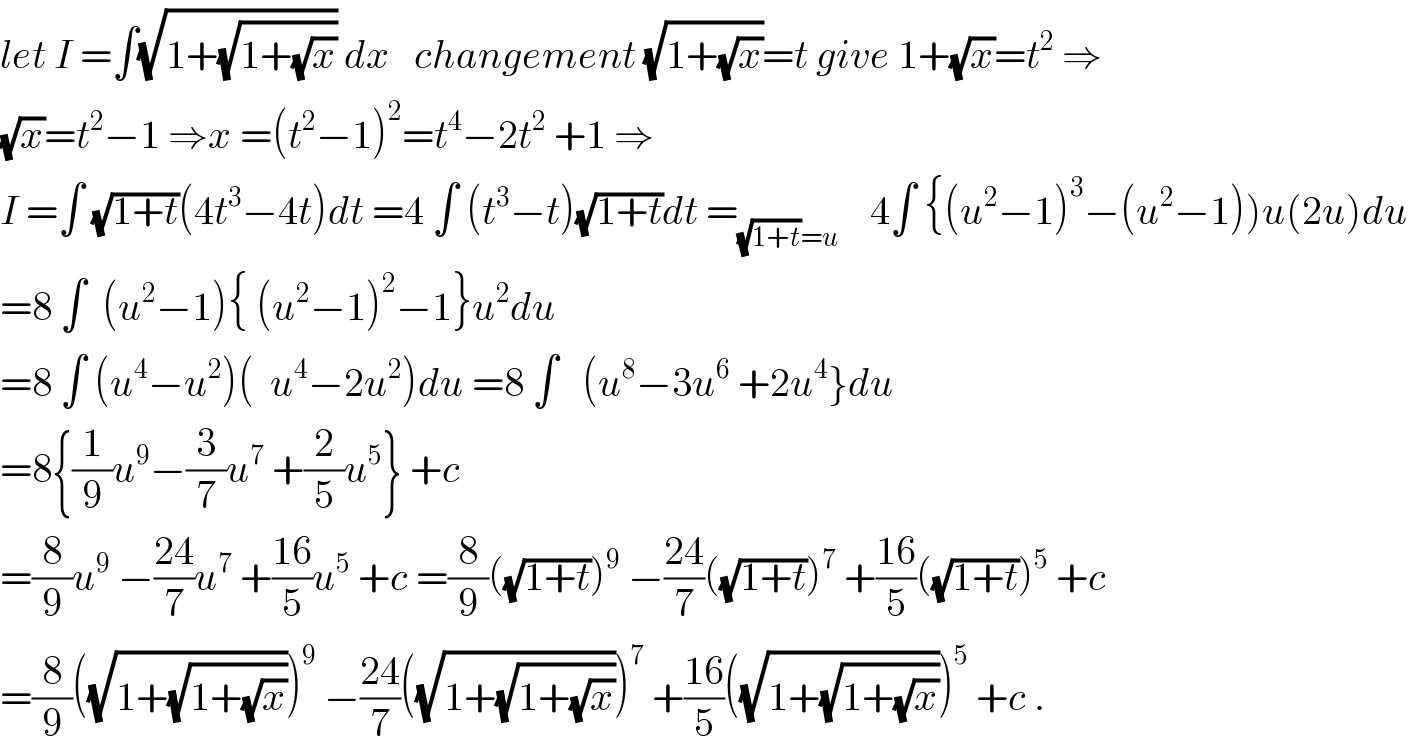
$let I =∫(√(1+(√(1+(√x))))) dx changement (√(1+(√x)))=t give 1+(√x)=t^2 ⇒ (√x)=t^2 −1 ⇒x =(t^2 −1)^2 =t^4 −2t^2 +1 ⇒ I =∫ (√(1+t))(4t^3 −4t)dt =4 ∫ (t^3 −t)(√(1+t))dt =_((√(1+t))=u) 4∫ {(u^2 −1)^3 −(u^2 −1))u(2u)du =8 ∫ (u^2 −1){ (u^2 −1)^2 −1}u^2 du =8 ∫ (u^4 −u^2 )( u^4 −2u^2 )du =8 ∫ (u^8 −3u^6 +2u^4 }du =8{(1/9)u^9 −(3/7)u^7 +(2/5)u^5 } +c =(8/9)u^9 −((24)/7)u^7 +((16)/5)u^5 +c =(8/9)((√(1+t)))^9 −((24)/7)((√(1+t)))^7 +((16)/5)((√(1+t)))^5 +c =(8/9)((√(1+(√(1+(√x))))))^9 −((24)/7)((√(1+(√(1+(√x))))))^7 +((16)/5)((√(1+(√(1+(√x))))))^5 +c .$
$l e t I = \int \sqrt{1 + \sqrt{1 + \sqrt{x}}} d x c h a n g e m e n t \sqrt{1 + \sqrt{x}} = t g i v e 1 + \sqrt{x} = t^{2} \Rightarrow$ $\sqrt{x} = t^{2} - 1 \Rightarrow x = {(t^{2} - 1)}^{2} = t^{4} - 2 t^{2} + 1 \Rightarrow$ $I = \int \sqrt{1 + t} (4 t^{3} - 4 t) d t = 4 \int (t^{3} - t) \sqrt{1 + t} d t =_{\sqrt{1 + t} = u} 4 \int {{(u^{2} - 1)}^{3} - (u^{2} - 1)) u (2 u) d u$ $= 8 \int (u^{2} - 1) {{(u^{2} - 1)}^{2} - 1} u^{2} d u$ $= 8 \int (u^{4} - u^{2}) (u^{4} - 2 u^{2}) d u = 8 \int (u^{8} - 3 u^{6} + 2 u^{4}} d u$ $= 8 {\frac{1}{9} u^{9} - \frac{3}{7} u^{7} + \frac{2}{5} u^{5}} + c$ $= \frac{8}{9} u^{9} - \frac{24}{7} u^{7} + \frac{16}{5} u^{5} + c = \frac{8}{9} {(\sqrt{1 + t})}^{9} - \frac{24}{7} {(\sqrt{1 + t})}^{7} + \frac{16}{5} {(\sqrt{1 + t})}^{5} + c$ $= \frac{8}{9} {(\sqrt{1 + \sqrt{1 + \sqrt{x}}})}^{9} - \frac{24}{7} {(\sqrt{1 + \sqrt{1 + \sqrt{x}}})}^{7} + \frac{16}{5} {(\sqrt{1 + \sqrt{1 + \sqrt{x}}})}^{5} + c .$
	Answered by tanmay.chaudhury50@gmail.com last updated on 05/Mar/19
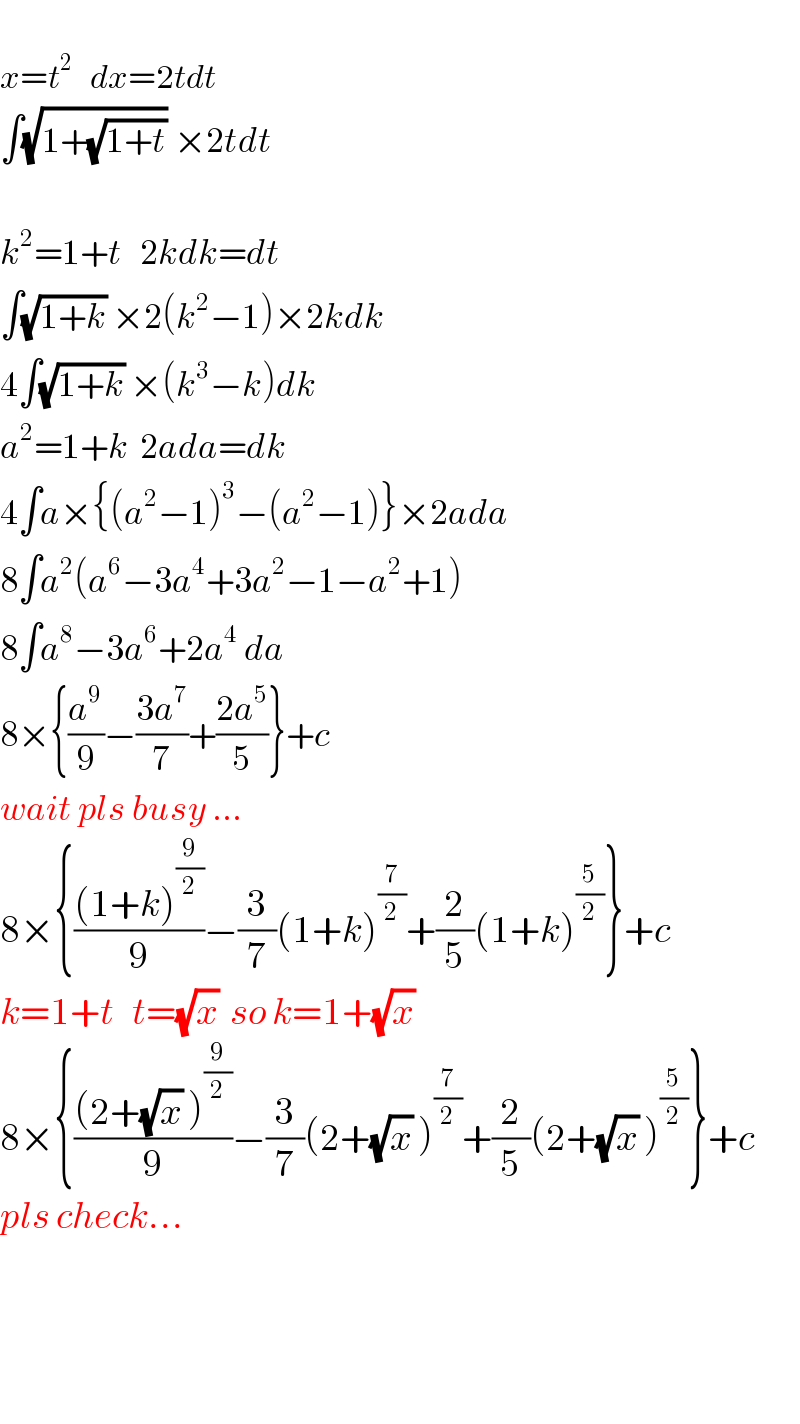
	$x=t^2 dx=2tdt ∫(√(1+(√(1+t)))) ×2tdt k^2 =1+t 2kdk=dt ∫(√(1+k)) ×2(k^2 −1)×2kdk 4∫(√(1+k)) ×(k^3 −k)dk a^2 =1+k 2ada=dk 4∫a×{(a^2 −1)^3 −(a^2 −1)}×2ada 8∫a^2 (a^6 −3a^4 +3a^2 −1−a^2 +1) 8∫a^8 −3a^6 +2a^4 da 8×{(a^9 /9)−((3a^7 )/7)+((2a^5 )/5)}+c wait pls busy ... 8×{(((1+k)^(9/2) )/9)−(3/7)(1+k)^(7/2) +(2/5)(1+k)^(5/2) }+c k=1+t t=(√x) so k=1+(√x) 8×{(((2+(√x) )^(9/2) )/9)−(3/7)(2+(√x) )^(7/2) +(2/5)(2+(√x) )^(5/2) }+c pls check...$
	$x = t^{2} d x = 2 t d t$ $\int \sqrt{1 + \sqrt{1 + t}} \times 2 t d t$ $k^{2} = 1 + t 2 k d k = d t$ $\int \sqrt{1 + k} \times 2 (k^{2} - 1) \times 2 k d k$ $4 \int \sqrt{1 + k} \times (k^{3} - k) d k$ $a^{2} = 1 + k 2 a d a = d k$ $4 \int a \times {{(a^{2} - 1)}^{3} - (a^{2} - 1)} \times 2 a d a$ $8 \int a^{2} (a^{6} - 3 a^{4} + 3 a^{2} - 1 - a^{2} + 1)$ $8 \int a^{8} - 3 a^{6} + 2 a^{4} d a$ $8 \times {\frac{a^{9}}{9} - \frac{3 a^{7}}{7} + \frac{2 a^{5}}{5}} + c$ $w a i t p l s b u s y . . .$ $8 \times {\frac{{(1 + k)}^{\frac{9}{2}}}{9} - \frac{3}{7} {(1 + k)}^{\frac{7}{2}} + \frac{2}{5} {(1 + k)}^{\frac{5}{2}}} + c$ $k = 1 + t t = \sqrt{x} s o k = 1 + \sqrt{x}$ $8 \times {\frac{{(2 + \sqrt{x})}^{\frac{9}{2}}}{9} - \frac{3}{7} {(2 + \sqrt{x})}^{\frac{7}{2}} + \frac{2}{5} {(2 + \sqrt{x})}^{\frac{5}{2}}} + c$ $p l s c h e c k . . .$
	Answered by MJS last updated on 05/Mar/19

	$\int \sqrt{1 + \sqrt{1 + \sqrt{x}}} d x =$ $[t = 1 + \sqrt{1 + \sqrt{x}} \to d x = 4 \sqrt{x} \sqrt{1 + \sqrt{x}} d t; \sqrt{x} = t^{2} - 2 t]$ $= 4 \int (t - 2) (t - 1) t^{\frac{3}{2}} d t =$ $= 4 \int (t^{\frac{7}{2}} - 3 t^{\frac{5}{2}} + 2 t^{\frac{3}{2}}) d t =$ $= \frac{8}{9} t^{\frac{9}{2}} - \frac{24}{7} t^{\frac{7}{2}} + \frac{16}{5} t^{\frac{5}{2}} =$ $= \frac{8}{315} t^{\frac{5}{2}} (35 t^{2} - 135 t + 126)$ $please do the inserting . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum