Question and Answers Forum

All Questions Topic List

IntegrationQuestion and Answers: Page 100

Question Number 132852 Answers: 0 Comments: 0

∫(x−1)^(x+1) dx

$\int {(x - 1)}^{x + 1} d x$

Question Number 132838 Answers: 1 Comments: 0

Question Number 132798 Answers: 2 Comments: 0

∫_0 ^(π/2) ((√(sin (x)))+(√(cos (x))))dx

${\int^{\frac{π}{2}}}_{0} (\sqrt{\sin (x)} + \sqrt{\cos (x)}) d x$

Question Number 132765 Answers: 2 Comments: 0

Question Number 132755 Answers: 3 Comments: 1

Question Number 132733 Answers: 1 Comments: 0

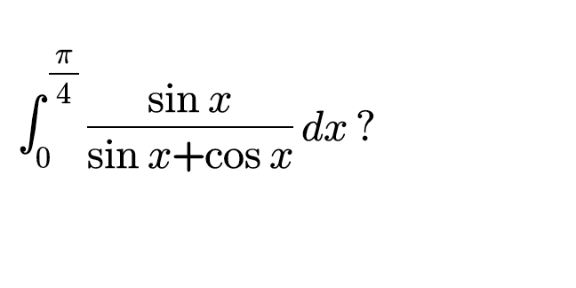
∫_0 ^∞ ((log x)/(1+x^2 +x^4 )) dx=...?

$\int_{0}^{\infty} \frac{\log x}{1 + x^{2} + x^{4}} d x = . . . ?$

Question Number 132729 Answers: 3 Comments: 0

....advanced calculus... evaluate : 𝛗=∫_0 ^( ∞) xe^(−2x) ln(x)dx=???

$. . . . a d v a n c e d c a l c u l u s . . .$ $e v a l u a t e :$ $ϕ = \int_{0}^{\infty} {x e}^{- 2 x} l n (x) d x = ? ? ?$

Question Number 132708 Answers: 2 Comments: 0

∫_(−∞) ^∞ ((x^2 cos (px+q))/(x^2 +(p+q)^2 ))dx

$\int_{- \infty}^{\infty} \frac{x^{2} \cos (p x + q)}{x^{2} + {(p + q)}^{2}} d x$

Question Number 132693 Answers: 2 Comments: 0

I=∫ (dx/(x(x^2 +1)^3 ))

$I = \int \frac{d x}{x {(x^{2} + 1)}^{3}}$

Question Number 132610 Answers: 2 Comments: 0

Ω=∫ ((sin^2 (x))/(1+sin^2 (x))) dx

$Ω = \int \frac{\sin^{2} (x)}{1 + \sin^{2} (x)} dx$

Question Number 132600 Answers: 0 Comments: 0

Question Number 132598 Answers: 0 Comments: 0

Find the voloume bounded by z=(√(x^2 +y^2 )) and the plane y+z=3

$Find the voloume bounded by z = \sqrt{x^{2} + y^{2}}$ $and the plane y + z = 3$

Question Number 132534 Answers: 3 Comments: 1

∫_0 ^(π/2) (dx/(1+sin x)) →diverges or converges?

$\int_{0}^{\frac{π}{2}} \frac{dx}{1 + \sin x} \to diverges or converges ?$

Question Number 132519 Answers: 1 Comments: 0

.... nice calculus.... prove that :: Σ_(n=1) ^∞ (((−1)^n ln(n))/n)=γln(2)−(1/2)ln^2 (2)

$. . . . n i c e c a l c u l u s . . . .$ $p r o v e t h a t ::$ $\underset{n = 1}{\sum^{\infty}} \frac{{(- 1)}^{n} l n (n)}{n} = γ l n (2) - \frac{1}{2} {l n}^{2} (2)$

Question Number 132473 Answers: 1 Comments: 0

∫ ((x cosh x)/((sinh x)^2 )) dx

$\int \frac{x \cosh x}{{(\sinh x)}^{2}} d x$

Question Number 132469 Answers: 1 Comments: 0

Question Number 132463 Answers: 1 Comments: 0

Given ∫_a ^( b) ((x^2 −3x)/(∣x−3∣)) dx = ((11)/2) where { ((a<3<b)),((a+2b=8)) :} Find ∫_a ^b ∣x∣ dx.

$Given \int_{a}^{b} \frac{x^{2} - 3 x}{∣ x - 3 ∣} dx = \frac{11}{2} where {\begin{cases} a < 3 < b \\ a + 2 b = 8 \end{cases}$ $Find \int_{a}^{b} ∣ x ∣ dx .$

Question Number 132414 Answers: 1 Comments: 1

Question Number 132410 Answers: 4 Comments: 0

∫_0 ^( ∞) (dx/((x^4 −x^2 +1)^2 ))

$\int_{0}^{\infty} \frac{dx}{{(x^{4} - x^{2} + 1)}^{2}}$

Question Number 132392 Answers: 0 Comments: 0

I = ∫e^(cos^(−1) x) dx = ?

$I = \int e^{\cos^{- 1} x} d x = ?$

Question Number 132376 Answers: 0 Comments: 0

∫_0 ^(π/2) ((sin(nx))/(sinx))dx

$\int_{0}^{\frac{π}{2}} \frac{\sin (nx)}{sinx} dx$

Question Number 132333 Answers: 2 Comments: 0

very nice integral ∫ ((4x^3 +4x^2 +4x+3)/((x^2 +1)(x^2 +x+1)^2 )) dx?

$very nice integral$ $\int \frac{{4 x}^{3} + {4 x}^{2} + 4 x + 3}{(x^{2} + 1) {(x^{2} + x + 1)}^{2}} dx ?$

Question Number 132324 Answers: 1 Comments: 0

....advanced calculus... evaluation : 𝛗=∫_(0^( ) ) ^( ∞) ((ln(1+x))/(x(1+x^2 ))) dx solution: 𝛗=[∫_0 ^( 1) ((ln(1+x))/(x(1+x^2 )))dx=𝛗_1 ]+[∫_1 ^( ∞) ((ln(1+x))/(x(1+x^2 ))) dx=𝛗_2 ] 𝛗_2 =^(x=(1/t)) ∫_0 ^( 1) ((ln(1+(1/t)))/((1/t)(1+(1/t^2 ))))(dt/t^2 )=∫_0 ^( 1) ((tln(1+(1/t)))/(1+t^2 ))dt =∫_0 ^( 1) ((tln(1+t))/(1+t^2 ))dt−∫_0 ^( 1) ((tln(t))/(1+t^2 ))dt ∴ 𝛗=𝛗_1 +𝛗_2 =∫_0 ^( 1) ((1/x)+x)((ln(1+x))/(1+x^2 ))dx−Φ 𝛗=∫_0 ^( 1) ((ln(1+x))/x)dx−Φ=−li_2 (−1)−Φ Φ=∫_0 ^( 1) ((xln(x))/(1+x^2 ))dx=Σ_(n=0) ^∞ ∫_0 ^( 1) (−1)^n x^(2n+1) ln(x)dx =Σ_(n=0) ^∞ (−1)^n {[(x^(2n+2) /(2n+2)) ln(x)]_0 ^1 −(1/(2n+2))∫_0 ^( 1) x^(2n+1) dx} =Σ_(n=0) ^∞ (−1)^(n+1) (1/(4(n+1)^2 ))=−(1/4) Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ) =((−1)/4) η(2)=((−π^2 )/(48)) .... ∴ 𝛗=−li_2 (−1)−Φ=(π^2 /(12))+(π^2 /(48)) 𝛗=((5π^2 )/(48))

$. . . . a d v a n c e d c a l c u l u s . . .$ $e v a l u a t i o n :$ $ϕ = \int_{0^{}}^{\infty} \frac{l n (1 + x)}{x (1 + x^{2})} d x$ $s o l u t i o n :$ $ϕ = [\int_{0}^{1} \frac{l n (1 + x)}{x (1 + x^{2})} d x = ϕ_{1}] + [\int_{1}^{\infty} \frac{l n (1 + x)}{x (1 + x^{2})} d x = ϕ_{2}]$ $ϕ_{2} \overset{x = \frac{1}{t}}{=} \int_{0}^{1} \frac{l n (1 + \frac{1}{t})}{\frac{1}{t} (1 + \frac{1}{t^{2}})} \frac{d t}{t^{2}} = \int_{0}^{1} \frac{t l n (1 + \frac{1}{t})}{1 + t^{2}} d t$ $= \int_{0}^{1} \frac{t l n (1 + t)}{1 + t^{2}} d t - \int_{0}^{1} \frac{t l n (t)}{1 + t^{2}} d t$ $∴ ϕ = ϕ_{1} + ϕ_{2} = \int_{0}^{1} (\frac{1}{x} + x) \frac{l n (1 + x)}{1 + x^{2}} d x - Φ$ $ϕ = \int_{0}^{1} \frac{l n (1 + x)}{x} d x - Φ = - {l i}_{2} (- 1) - Φ$ $Φ = \int_{0}^{1} \frac{x l n (x)}{1 + x^{2}} d x = \underset{n = 0}{\sum^{\infty}} \int_{0}^{1} {(- 1)}^{n} x^{2 n + 1} l n (x) d x$ $= \underset{n = 0}{\sum^{\infty}} {(- 1)}^{n} {{[\frac{x^{2 n + 2}}{2 n + 2} l n (x)]}_{0}^{1} - \frac{1}{2 n + 2} \int_{0}^{1} x^{2 n + 1} d x}$ $= \underset{n = 0}{\sum^{\infty}} {(- 1)}^{n + 1} \frac{1}{4 {(n + 1)}^{2}} = - \frac{1}{4} \underset{n = 1}{\sum^{\infty}} \frac{{(- 1)}^{n - 1}}{n^{2}}$ $= \frac{- 1}{4} η (2) = \frac{- π^{2}}{48} . . . .$ $∴ ϕ = - {l i}_{2} (- 1) - Φ = \frac{π^{2}}{12} + \frac{π^{2}}{48}$ $ϕ = \frac{5 π^{2}}{48}$

Question Number 132302 Answers: 1 Comments: 0

Simplify ((𝚪((p/2))𝚪((1/2)))/(𝚪((p/2)+(1/2))))

$Simplify$ $\frac{Γ (\frac{p}{2}) Γ (\frac{1}{2})}{Γ (\frac{p}{2} + \frac{1}{2})}$

Question Number 132301 Answers: 0 Comments: 0

..... nice.......calculus.... prove that :: ∫_0 ^( ∞) ((sin(2arctan((x/2))))/((x^2 +2^2 )sinh(πx)))dx=(7/8) −(π^2 /(12))

$. . . . . n i c e . . . . . . . c a l c u l u s . . . .$ $p r o v e t h a t ::$ $\int_{0}^{\infty} \frac{s i n (2 a r c t a n (\frac{x}{2}))}{(x^{2} + 2^{2}) s i n h (π x)} d x = \frac{7}{8} - \frac{π^{2}}{12}$

Question Number 132235 Answers: 1 Comments: 0

I= ∫ ((3x+5)/((x^2 +2x+3)^2 )) dx ?

$I = \int \frac{3 x + 5}{{(x^{2} + 2 x + 3)}^{2}} dx ?$

Pg 95 Pg 96 Pg 97 Pg 98 Pg 99 Pg 100 Pg 101 Pg 102 Pg 103 Pg 104

Contact: info@tinkutara.com