
Question and Answers Forum
IntegrationQuestion and Answers: Page 108



Pg 103 Pg 104 Pg 105 Pg 106 Pg 107 Pg 108 Pg 109 Pg 110 Pg 111 Pg 112
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 108 |
| please answer my question |
| ∫_1 ^a ((4(√x) +k)/( (√x) +1)) = 4a+3 . Find the value of ∫_1 ^( a) (1/( (√x) +1)) dx . |
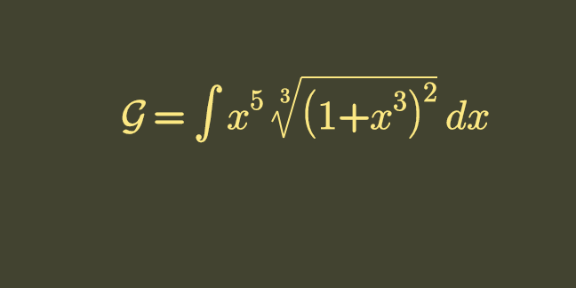
|
| ∫e^x^x dx please help me |
| V=∫_0 ^( 1) arctan ((x/y)) dx ? |
| H = ∫ tan x tan 2x tan 3x dx ? |
| W = ∫ ((cos 5x+cos 4x)/(2cos 3x−1)) dx |
| M = ∫ (√(x+(√(x^2 +5)))) dx ? |
| ... nice calculus... calculate:: φ=^(???) ∫_0 ^( (π/4)) (dx/((sin(x)+cos(x)+(√2) )^2 )) |
| G = ∫ ((sin^2 x+sin x)/(1+sin x+cos x)) dx ? |
| J = ∫ (dθ/(tan θ+cot θ+sec θ+csc θ)) ? |

|

|
| ∫_0 ^( x) (x−u)^2 u f(u) du = 4x−6sin x+2xcos x f(x)=? |

|
| valuate the following integral I=∫_1 ^∞ (dt/((t)^(2k+v+(3/2)) (√(t−1)))) and prove that: I=(√π)((Γ(v+1))/(Γ(v+(3/2)))) ((((((v+1)/2))_k (1+(v/2))_k )/(((v/2)+(3/4))_k ((v/2)+(5/4))_k ))) |
| φ = ∫ ((ln (x))/x^2 ) dx |
| ∫_1 ^∞ (1/(1+x^3 ))dx = ... |
| ∫ ((5e^(4t) +10e^(2t) +2)/(e^(2t) +2)) dt |
| prove using the first principle that the derivative of sin x is cox x and that the derivative of cos x is −sinx |
| Given that tan^(−1) x show that (dy/dx) = (1/(1+x^2 )) |
| ∫_(−(1/2)) ^( −(1/4)) x(x+1) (√(1+(1/x^2 )+(1/((x+1)^2 )))) dx =? |
| Given f(x+1)=((1+f(x))/(1−f(x))) ; f(2)=2 and ∫_2 ^( 2018) x.f(2018)dx=2^a .3^b .5^c .7^d .11^e .101^f then a+b+c+d+e +f=__ |
| ∫_1 ^∞ (dx/(1+x^4 )) = ... |
| ∫ ln (tan x) ln (sin x) dx ? |
| ∫ ((√x)/(x−1)) dx =? |
Pg 103 Pg 104 Pg 105 Pg 106 Pg 107 Pg 108 Pg 109 Pg 110 Pg 111 Pg 112 |