
Question and Answers Forum
IntegrationQuestion and Answers: Page 112

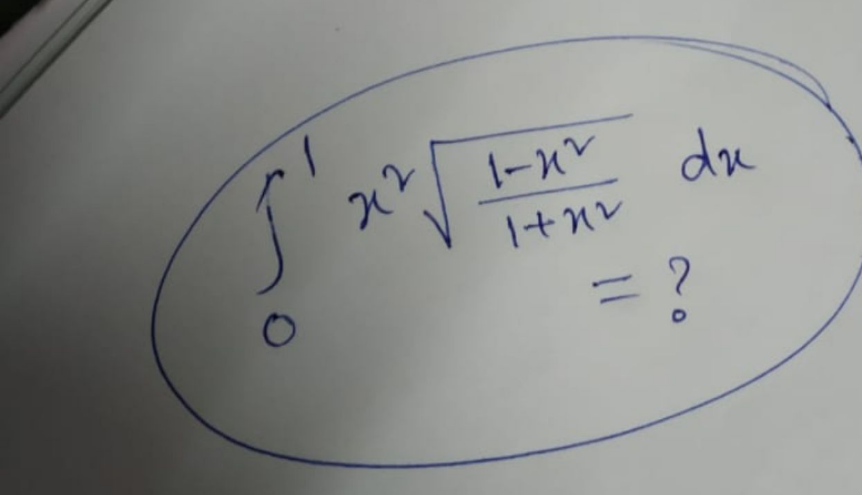

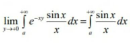

Pg 107 Pg 108 Pg 109 Pg 110 Pg 111 Pg 112 Pg 113 Pg 114 Pg 115 Pg 116
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 112 |
| ∫_0 ^( 1) ∫_0 ^( 1) (1/(1−xy^2 )) dx dy =? |
| I = ∫ arctan (((x−2)/(x+2))) dx |
| ∫_(π/2) ^((2π)/3) (((arcsinhx)^2 )/(2cosx))dx |
|
| ....nice calculus...= Titu′s lemma:: for any positive numbers : a_1 ,a_2 ,...,a_n , b_1 ,b_2 ,...,b_n we have: (((a_1 +...+a_n )^2 )/(b_1 +...+b_n ))≤(a_1 ^2 /b_1 ) +...+(a_n ^2 /b_n ) proof : put : x=(x_1 ,...,x_n )∈R^n :y=(y_1 ,...,y_n )∈R^n (x.y)^2 ≤∣x∣^2 ∣y∣^2 (cauchy−schwarz inequality) (x_1 y_1 +...+x_n y_n )^2 ≤(x_(1 ) ^2 +...+x_n ^2 )(y_1 ^2 +...+y_(n ) ^2 ) by applying subsitution : x_i =(a_i /( (√b_i ))) , y_i =(√b_i ) (i=1,2 ,...,n) ((a_(1 ) ^2 +...+a_(n ) ^2 )/(b_2 +...+b_n ))≤(a_1 ^2 /b_1 )+...+(a_n ^2 /b_n ) ✓✓ |
| ...nice calculus... calculate Ω=∫_1 ^( ∞) ((ln(x^4 −2x^2 +2))/(x(√(x^2 −1)) )) dx=? |

|
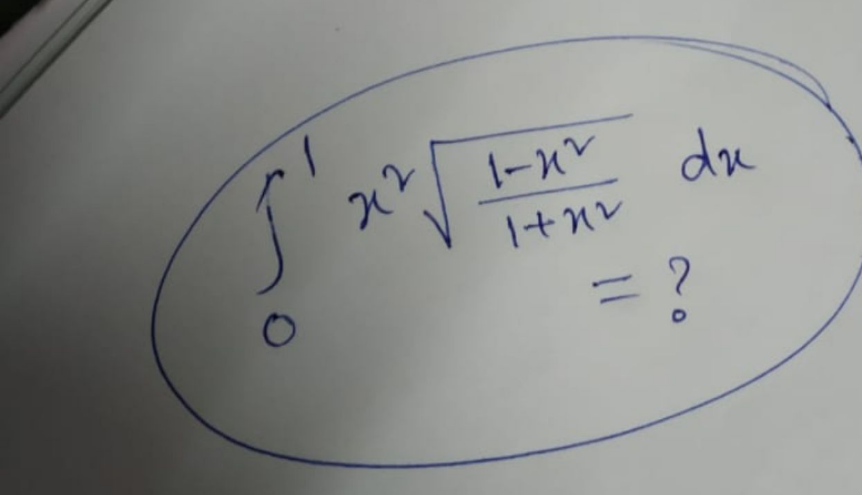
|
| find F(a)=∫_0 ^1 (√((1+a^2 t^2 )/(1−t^2 ))) dt for background see Q127811. |
| prove that ∫_0 ^( 100) (dx/( (√(x(100−x))))) = π |
| ∫(((sin (2tan^(−1) (x)+x))/x)) the limit [0,∞) |
| 2021 HAPPY NEW Year 1)∫((x^3 +3x+2)/((x^2 +1)^2 (x+1)))dx 2)∫((2cos(x)−sin(x))/(3sin(x)+5cos(x)))dx 3)∫((tan(2x))/( (√(sin^6 (x)+cos^6 (x)))))dx 4)∫x(√((1−x^2 )/(1+x^2 ))) dx |
| ∫(√x)e^x dx ? |
| ψ = ∫ (dx/(x^3 (((x^5 +1)^3 ))^(1/5) )) ? |

|
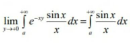
|

|
| find A_n = ∫_0 ^(+∞) (dx/((x^2 +1)^n )) |
| explicite f(a)=∫_0 ^∞ ((lnx)/(x^2 −x+a))dx with a>(1/4) |
| calculate ∫_0 ^∞ ((lnx)/((x^2 −x+1)^2 ))dx |
| prove that ∫_0 ^∞ e^(−x) lnxdx=−γ |
| calculate u_n =∫_0 ^1 x^n (√(1−x^4 ))dx |
| calculate ∫_0 ^(2π) (dx/((cosx +2sinx)^2 )) |
| z=x+iy why ((f(z))/(z−a)) not analytical? / not analytical at z=a? |
| if f(x)= { ((x−n ; 2n ≤ x ≤2n+1)),((n+1 ; 2n+1≤x≤2n+2 )) :} where n =0,1,2,3,..,9 find ∫_0 ^(20) f(x)dx |
| its 9:30pm in Cameroon |
Pg 107 Pg 108 Pg 109 Pg 110 Pg 111 Pg 112 Pg 113 Pg 114 Pg 115 Pg 116 |