
Question and Answers Forum
IntegrationQuestion and Answers: Page 115



Pg 110 Pg 111 Pg 112 Pg 113 Pg 114 Pg 115 Pg 116 Pg 117 Pg 118 Pg 119
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 115 |
| ∫ ((tan(x))/x) dx |
| evaluate :: ∫_(−1) ^( 0) (dx/( ((1+x^3 ))^(1/3) )) =? |
| ∫_( (√2)) ^(2e^(√2) ) ln (((e^x +e^(−x) )/(9(√x))))dx ? |
| ∫(1/dx)=? |
| ∫ (dx/((1+x^2 )(√(1−x^2 )))) ? |
| ∫_( 0) ^( (√(ln (π/2)))) xe^x^2 sin (e^x^2 ) dx ? |
| ... advanced calculus... prove that ::: ((Γ(((1−x)/2))Γ(x))/(Γ((x/2)))) =^(???) ((2^(x−1) (√π))/(cos(((πx)/2)))) |
| ...nice calculus... calculate ::: Ω=^(???) ∫_0 ^( ∞) e^( −t) t^( 2) j_0 ( t )dt where : j_((v)) (x)=x^v Σ_(n=0) ^( ∞) (((−1)^n x^(2n) )/(2^(2n+v) n!Γ(n+v+1))) ::: Bessel function of the first type of order v ... j_v (x) is convergent (why?): ∀x∈R... |
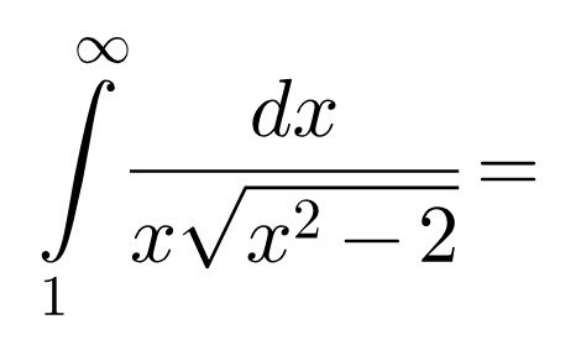
|

|
| solve ∫_0 ^( 1) ((1−x^2 )/((1+x^2 )(√(1+x^4 )))) dx ? |
| ∫ e^( cos^(− 1) (x)) dx |
| calculate ∫∫ _([0,1]^2 ) ((dxdy)/( (√(x^2 +y^2 )) +xy)) |
| ∫_0 ^∞ (1/(1+x^s +x^(2s) )) |
| ∫_0 ^( ∞) ((e^(2πx) −1)/(e^(2πx) +1)) ((1/x)−(1/(N^2 +x^2 ))) dx |
| let f(x)= e^(−2x) actan (3x+1) 1)calculste f^((n)) (x) and f^((n)) (0) 2) if f(x)=Σ a_n x^n determine the sequence a_n 3) calculate ∫_0 ^∞ f(x)dx |
| closed formula .... ∫_0 ^( 1) ((x^n ln(x))/(1+x))dx =? |

|

|

|
| Show that:: Ω = ∫_0 ^( 1) ((Li_2 (x)log(x))/(1+x))dx = −(3/(16))ζ(4) Goodluck |
| ∫ (dx/((x−1)(√(x^2 −2x)))) ? |

|
| Find the Riemann sum for the given function with the specified number of intervals using left endpoints f(x)= 4ln x+2x ; 1≤x≤4 n=7 . Round your answer to two decimal places ? |

|
| ∫ cot x ln (sin x) dx ? |
Pg 110 Pg 111 Pg 112 Pg 113 Pg 114 Pg 115 Pg 116 Pg 117 Pg 118 Pg 119 |