
Question and Answers Forum
IntegrationQuestion and Answers: Page 118






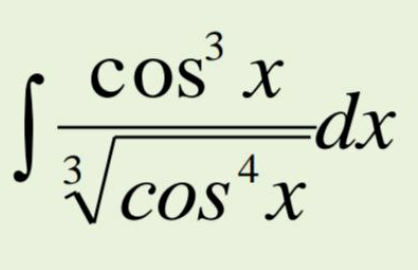
Pg 113 Pg 114 Pg 115 Pg 116 Pg 117 Pg 118 Pg 119 Pg 120 Pg 121 Pg 122
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 118 |
| find ∫_0 ^∞ ((x^3 sin(2x))/((x^2 +x+1)^3 ))dx |
| φ(α) = ∫ ((6α^2 +30α+2)/(4α^2 +20α+25)) dα |
| ∫ ((sin x cos x)/(1−2cos 2x)) dx |
| find ∫_0 ^∞ ((xarctanx)/((x^(2 ) +1)^2 ))dx |

|
| ∫ (dx/( ((tan x))^(1/3) )) ? |
| ∫_( 0) ^( ∞) (x^2 /((1+x^2 )^2 )) dx |

|
| ∫(√(x^3 +ax+b))dx |

|
| ...nice calculus... prove that:: ∫_((−π)/4) ^(π/4) (((π−4x)tan(x))/(1−tan(x)))dx=^(???) πln(2)−(π^2 /4) |
| ∫ (1/( (√x) (x+1)((tan^(−1) (√x))^2 +9)))dx |
| ... advanced integral... prove that :: Ω=∫_0 ^( ∞) ((sin^2 (x))/(x^2 (1+x^2 )))dx =(π/4)(1+(π/e^2 )) |
| ∫_0 ^π ((sin^2 x)/( (√x))) dx |
| ∫ (((x−1)(√(x^4 +2x^3 −x^2 +2x+1)))/(x^2 (x+1))) dx ? |
| To mr mjs sir. integral lover ∫_0 ^(π/4) ((tan ((π/4)−x))/(cos^2 x (√(tan^3 x+tan^2 x+tan x)))) dx =? |
| ∫sect e^t dt |
| ∫ ((4x−1)/(2x^2 −3x+2)) dx ? |

|

|

|
| .... advanced calculus ... prove that:::: Σ_(n=1) ^∞ {((ζ(2n+1))/(4^(n ) (2n+1)))}=ln(2)−γ γ:: euler−mascheroni constant |
| ...advanced calculus... evaluation of: Ω=∫_0 ^( (π/2)) sin(x)log(sin(x))dx by using the euler beta and gamma function: β(p,(1/2))=2∫_0 ^(π/2) sin^(2p−1) (x)dx ((dβ(p,(1/2)))/dp) =2∫_0 ^(π/2) 2sin^(2p−1) (x)ln(sin(x))dx =4∫_0 ^(π/2) sin^(2p−1) (x)ln(sin(x))dx Ω=(1/4)[((dβ(p,(1/2)))/dp)]_(p=1) ((d(β(p,(1/2))))/dp)=(√π)[((Γ′(p)Γ(p+(1/2))−Γ′(p+(1/2))Γ(p))/(Γ^2 (p+(1/2))))]_(p=1) Ω=(1/4)((√π)[((Γ^′ (1)Γ((3/2))−Γ′((3/2))Γ(1))/(Γ^2 ((3/2))))]) =((√π)/4)[((−γ(((√π)/2))−((√π)/2)(2−γ−2ln(2)))/(π/4))] =((√π)/4)∗((√π)/2)(((−γ−2+γ+2ln(2))/(π/4))) =ln(2)−1 ... m.n.july.1970... |
| calculate ∫_1 ^(√3) (dx/((x^2 +1)^2 (x+2)^5 )) |
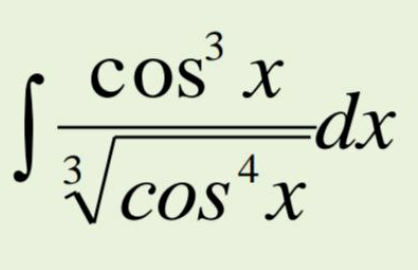
|
| find ∫_0 ^∞ e^(−x) ln(1+e^(2x) )dx |
Pg 113 Pg 114 Pg 115 Pg 116 Pg 117 Pg 118 Pg 119 Pg 120 Pg 121 Pg 122 |