Question and Answers Forum

All Questions Topic List

IntegrationQuestion and Answers: Page 120

Question Number 122927 Answers: 1 Comments: 1

Question Number 122922 Answers: 1 Comments: 0

∫_0 ^(π/4) ((cos x+sin x)/(16sin 2x+9)) dx

$\underset{0}{\int^{π / 4}} \frac{\cos x + \sin x}{16 \sin 2 x + 9} d x$

Question Number 122919 Answers: 2 Comments: 0

Question Number 122885 Answers: 3 Comments: 1

Question Number 122884 Answers: 1 Comments: 1

Question Number 122882 Answers: 1 Comments: 0

... nice calculus... prove that ::: Ω=∫_0 ^( 1) (((x^ϕ −1)/(ln(x))))^2 dx=(√5) ln(ϕ) .m.n.

$. . . n i c e c a l c u l u s . . .$ $p r o v e t h a t :::$ $Ω = \int_{0}^{1} {(\frac{x^{φ} - 1}{l n (x)})}^{2} d x = \sqrt{5} l n (φ)$ $. m . n .$

Question Number 122877 Answers: 1 Comments: 1

∫ (sin^(−1) (x))^2 dx ?

$\int {(\sin^{- 1} (x))}^{2} d x ?$

Question Number 122875 Answers: 1 Comments: 0

∫(((x^2 +1)dx)/(x^4 +x^2 +1)) = ...

$\int \frac{(x^{2} + 1) dx}{x^{4} + x^{2} + 1} = . . .$

Question Number 122867 Answers: 2 Comments: 0

Question Number 122853 Answers: 0 Comments: 2

Question Number 122838 Answers: 1 Comments: 0

∫ (dx/( (((x−1)^3 (x+2)^5 ))^(1/4) )) ?

$\int \frac{d x}{\sqrt[4]{{(x - 1)}^{3} {(x + 2)}^{5}}} ?$

Question Number 122828 Answers: 1 Comments: 0

Question Number 122823 Answers: 1 Comments: 0

Question Number 122822 Answers: 1 Comments: 0

Question Number 122807 Answers: 1 Comments: 1

Question Number 122751 Answers: 3 Comments: 0

∫_0 ^(1/(√2)) ((x sin^(−1) (x^2 ))/( (√(1−x^4 )))) dx ?

$\underset{0}{\int^{1 / \sqrt{2}}} \frac{x \sin^{- 1} (x^{2})}{\sqrt{1 - x^{4}}} d x ?$

Question Number 122748 Answers: 3 Comments: 0

∫_0 ^3 (dx/((3−x)(√(x^2 +1)))) ?

$\underset{0}{\int^{3}} \frac{d x}{(3 - x) \sqrt{x^{2} + 1}} ?$

Question Number 122734 Answers: 1 Comments: 0

Question Number 122713 Answers: 0 Comments: 0

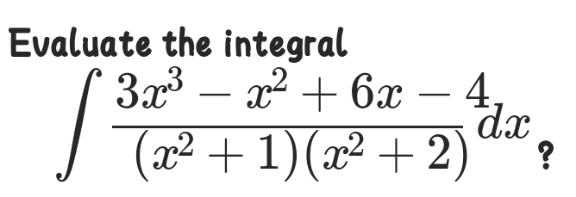
... advanced math ... two simple and nice integrals: prove that:: Ω_1 =∫_0 ^( ∞) ((sin(e^(−γ) x)ln(x))/x) dx=0 Ω_2 =∫_0 ^( ∞) ((sin(x^((√2)/2) )ln(x))/x)dx=−πγ note :: γ : Euler−mascheroni constant. .m.n.

$. . . a d v a n c e d m a t h . . .$ $t w o s i m p l e a n d n i c e i n t e g r a l s :$ $p r o v e t h a t ::$ $Ω_{1} = \int_{0}^{\infty} \frac{s i n (e^{- γ} x) l n (x)}{x} d x = 0$ $Ω_{2} = \int_{0}^{\infty} \frac{s i n (x^{\frac{\sqrt{2}}{2}}) l n (x)}{x} d x = - π γ$ $n o t e :: γ : E u l e r - m a s c h e r o n i$ $c o n s t a n t .$ $. m . n .$

Question Number 122697 Answers: 3 Comments: 0

∫ (dx/( (√((x−a)(b−x))))) ?

$\int \frac{d x}{\sqrt{(x - a) (b - x)}} ?$

Question Number 122689 Answers: 1 Comments: 0

Evaluate the integral ∫ (((x)^(1/3) +1)/( (x)^(1/3) −1)) dx

$E v a l u a t e t h e i n t e g r a l$ $\int \frac{\sqrt[3]{x} + 1}{\sqrt[3]{x} - 1} d x$

Question Number 122671 Answers: 1 Comments: 2

...nice integral... prove that :: ∫_0 ^( ∞) cos(πnx)((1/x^2 )−((πcoth(πx))/x))dx =^(???) πln(1−e^(−πn) ) .m.n.

$. . . n i c e i n t e g r a l . . .$ $p r o v e t h a t ::$ $\int_{0}^{\infty} c o s (π n x) (\frac{1}{x^{2}} - \frac{π c o t h (π x)}{x}) d x$ $\overset{? ? ?}{=} π l n (1 - e^{- π n})$ $. m . n .$

Question Number 122636 Answers: 1 Comments: 0

...nice calculus... In AB^Δ C prove :: ∗: sin((A/2))sin((B/2))sin((C/2))≤(1/8) ......................... ∗∗:: max(cos((A/2))cos((B/2))cos((C/2)))=?

$. . . n i c e c a l c u l u s . . .$ $I n A \overset{Δ}{B C} p r o v e ::$ $* : s i n (\frac{A}{2}) s i n (\frac{B}{2}) s i n (\frac{C}{2}) ⩽ \frac{1}{8}$ $. . . . . . . . . . . . . . . . . . . . . . . . .$ $* * :: m a x (c o s (\frac{A}{2}) c o s (\frac{B}{2}) c o s (\frac{C}{2})) = ?$

Question Number 122631 Answers: 2 Comments: 2

solve ∫_((a−1)^2 ) ^a^2 cosh^(−1) (1/( (√(a−(√x))))) dx with a>0

$solve \underset{{(a - 1)}^{2}}{\int^{a^{2}}} \cosh^{- 1} \frac{1}{\sqrt{a - \sqrt{x}}} d x with a > 0$

Question Number 122626 Answers: 2 Comments: 0

Question Number 122625 Answers: 0 Comments: 0

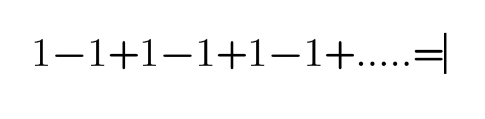
... advanced integral... i: ∫_0 ^( 1) ((1/(ln(x)))+(1/(1−x)))dx=γ ii: ψ(x)=∫_0 ^( ∞) ((e^(−t) /t) −(e^(−tx) /(1−e^(−t) )))dt solution :{_(2 : ln(n) =^(easy) ∫_0 ^( 1) ((x^(n−1) −1)/(ln(x)))dx (∗∗)) ^(1: H_n = Σ_(k=1) ^n (1/k) =∫_0 ^( 1) ((1−x^n )/(1−x)) dx (∗)) (∗)−(∗∗): H_n −ln(n)=∫_0 ^1 (((1−x^n )/(1−x)) −((x^(n−1) −1)/(ln(x))))dx lim_(n→∞) (x^n )=^(0<x<1) 0 lim_(n→∞) (H_n −ln(n))=∫_0 ^( 1) ((1/(1n(x)))+(1/(1−x)))dx γ= ∫_0 ^( 1) ((1/(ln(x)))+(1/(1−x)))dx ✓ ............................. ψ(x)=^(easy) −γ+∫_0 ^( 1) ((1−t^(x−1) )/(1−t))dt ψ(x)=−∫_0 ^( 1) (1/(ln(t)))+(1/(1−t))dt+∫_0 ^( 1) ((1−t^(x−1) )/(1−t))dt =∫_0 ^( 1) −(1/(ln(t))) +((1−t^(x−1) −1)/(1−t))dt =−∫_0 ^( 1) (1/(ln(t)))+(t^(x−1) /(1−t)) dt=^(t=e^(−y) ) =−∫_∞ ^( 0) ((1/(−y))+(e^(−yx+y) /(1−e^(−y) )))(−e^(−y) )dy =∫_0 ^( ∞) (e^(−y) /y)−(e^(−yx) /(1−e^(−y) ))dy ∵ ψ(x)=∫_0 ^( ∞) ((e^(−y) /y)−(e^(−yx) /(1−e^(−y) )))dy ✓

$. . . a d v a n c e d i n t e g r a l . . .$ $i : \int_{0}^{1} (\frac{1}{l n (x)} + \frac{1}{1 - x}) d x = γ$ $i i : ψ (x) = \int_{0}^{\infty} (\frac{e^{- t}}{t} - \frac{e^{- t x}}{1 - e^{- t}}) d t$ $s o l u t i o n : {_{2 : l n (n) \overset{e a s y}{=} \int_{0}^{1} \frac{x^{n - 1} - 1}{l n (x)} d x (* *)}^{1 : H_{n} = \underset{k = 1}{\sum^{n}} \frac{1}{k} = \int_{0}^{1} \frac{1 - x^{n}}{1 - x} d x (*)}$ $(*) - (* *) : H_{n} - l n (n) = \int_{0}^{1} (\frac{1 - x^{n}}{1 - x} - \frac{x^{n - 1} - 1}{l n (x)}) d x$ ${l i m}_{n \to \infty} (x^{n}) \overset{0 < x < 1}{=} 0$ ${l i m}_{n \to \infty} (H_{n} - l n (n)) = \int_{0}^{1} (\frac{1}{1 n (x)} + \frac{1}{1 - x}) d x$ $γ = \int_{0}^{1} (\frac{1}{l n (x)} + \frac{1}{1 - x}) d x ✓$ $. . . . . . . . . . . . . . . . . . . . . . . . . . . . .$ $ψ (x) \overset{e a s y}{=} - γ + \int_{0}^{1} \frac{1 - t^{x - 1}}{1 - t} d t$ $ψ (x) = - \int_{0}^{1} \frac{1}{l n (t)} + \frac{1}{1 - t} d t + \int_{0}^{1} \frac{1 - t^{x - 1}}{1 - t} d t$ $= \int_{0}^{1} - \frac{1}{l n (t)} + \frac{1 - t^{x - 1} - 1}{1 - t} d t$ $= - \int_{0}^{1} \frac{1}{l n (t)} + \frac{t^{x - 1}}{1 - t} d t \overset{t = e^{- y}}{=}$ $= - \int_{\infty}^{0} (\frac{1}{- y} + \frac{e^{- y x + y}}{1 - e^{- y}}) (- e^{- y}) d y$ $= \int_{0}^{\infty} \frac{e^{- y}}{y} - \frac{e^{- y x}}{1 - e^{- y}} d y$ $∵ ψ (x) = \int_{0}^{\infty} (\frac{e^{- y}}{y} - \frac{e^{- y x}}{1 - e^{- y}}) d y ✓$

Pg 115 Pg 116 Pg 117 Pg 118 Pg 119 Pg 120 Pg 121 Pg 122 Pg 123 Pg 124

Contact: info@tinkutara.com